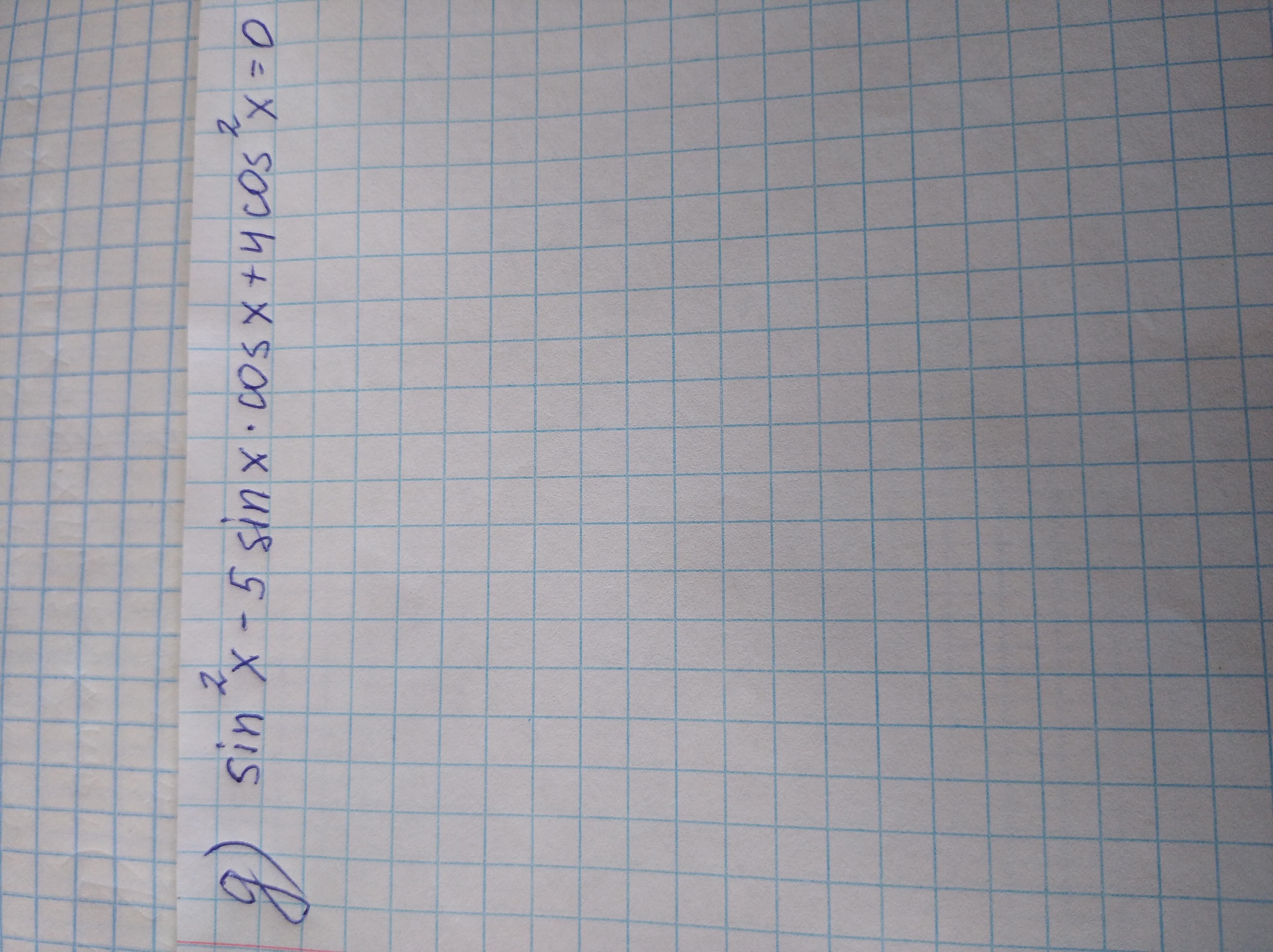Предмет: Математика
Автор: zaporozcevaanastasia
Вопрос задан 6 лет назад

< >

ПОМОГИТЕ РЕШИТЬ УРАВНЕНИЯ

Приложения:

Ответы

Ответ дал: ismars

0

$\sin^2x-5 \sin x \cdot \cos x + 4 \cos^2 x=0\\$

$\cos x \neq 0,$ так как иначе квадрат синуса будет равен единице из основного тригонометрического тождества, и равенство будет неверным. Поэтому можем разделить обе части на квадрат косинуса:

$tg^2(x)-5tg(x)+4=0\\(tg(x)-1)(tg(x)-4)=0\\\left \{ {{tg(x)=1} \atop {tg(x)=4}} \right.\\ \left \{ {{x=\frac{\pi}{4}+\pi n, n \in Z } \atop {x=arctg(4)+\pi n, n \in Z}} \right.$

Похожие вопросы

Английский язык

1 год назад

Помогите пожалуйста

Английский язык

1 год назад

Укажите, какое предложение грамматически верное, а какое нет, 1-CORRECT или 2-NOT CORRECT А)There was wonderful scenery from my hotel room. В)There was a wonderful view from my hotel room.

Английский язык

2 года назад

помогите!! задали по английскому сочинение " Человек которым я восхищаюсь" 220-250 слов нигде в интернете не могу найти!

Русский язык

2 года назад

Живописны . Как проверить букву с ?

Геометрия

7 лет назад

допоможіть будь ласка, завдання 3 і 4

Алгебра

7 лет назад

График функций можно рисунки ПОЖАЛУЙСТА помогите и можно полностью решение.

Геометрия

9 лет назад

признак равенства прямоугольных треугольников по катету и острому углу

Алгебра

9 лет назад

Ребят,АЛГЕБРА,в теме не аллё.С полным решением:)