Расстояние между центрами двух окружностей равно d и меньше разности R3 - R, их радиусов (R. > R,). Найдите най- меньшее и наибольшее расстояния между точками, располо- женными на данных окружностях. ​

Ответ:

Если бы расстояние между центрами равнялось разности радиусов:
d = R1 - R2
То малая окружность касалась бы большой изнутри.
А так как O1O2 = d < R1 - R2, то она находится внутри большой, но не касается.
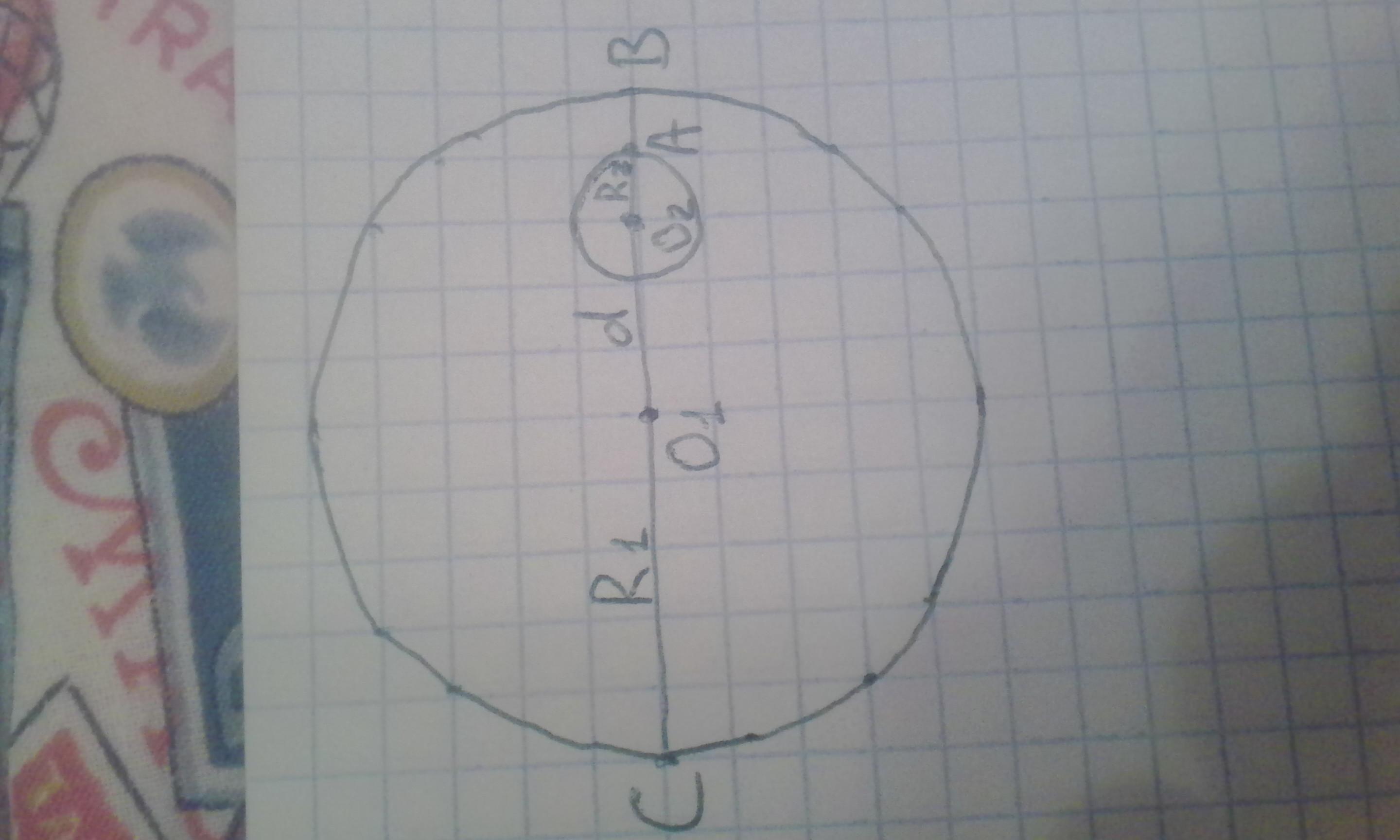
Наименьшее расстояние между точками окружностей
AB = R1 - R2 - d
Наибольшее расстояние между точками окружностей
AC = R1 + R2 + d
Смотри рисунок.

Объяснение: