Предмет: Алгебра
Автор: Аноним
Вопрос задан 6 лет назад

< >

с полным решением пожалуйста

Приложения:

Ответы

Ответ дал: sangers1959

1

Объяснение:

3.1

$y(x)=5^{\frac{7}{2x-3} }.$

ОДЗ: 2х-3≠0 2х≠3 |:2 x≠1,5. ⇒

Точка х₀=1,5 - точка разрыва.

Исследуем эту точку:

$\lim\limits_{x \to 1,5-0} 5^{\frac{7}{2x-3}} =0.\ \ \ (5^\frac{7}{2*1,5-0-3}=5^\frac{7}{3-0-3}=5^\frac{7}{-0}=(\frac{1}{5})^\frac{7}{0} =(\frac{1}{5})^{\infty}=0) \\ \lim\limits_{x \to 1,5+0} 5^{\frac{7}{2x-3}} =\infty.\ \ \ \ (5^\frac{7}{2*1,5+0-3}=5^\frac{7}{3+0-3}=5^\frac{7}{0}=5^{\infty}=\infty).\ \ \ \ \Rightarrow\\$

x₀=1,5 - это точка разрыва второго рода.

3.2

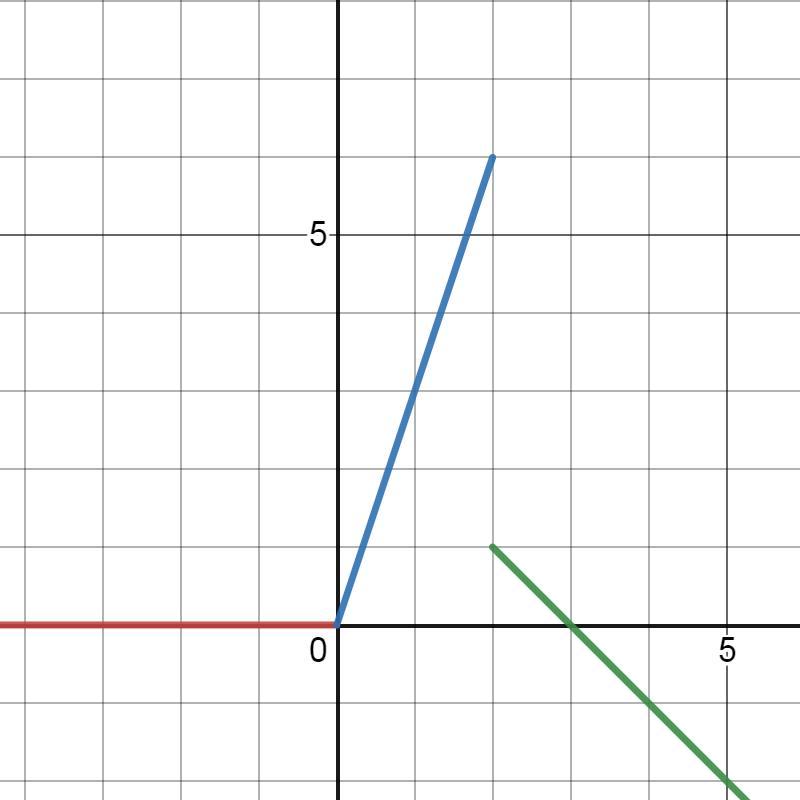
$y(x)=\left\{\begin{array}{ccc}0,\ \ x\leq 0\\3x,\ \ 0 < x < 2\\3-x,\ \ \ x\geq 2\end{array}\right..$

$x_0=0.\\ \lim\limits_{x \to 0-0} 0=0.\\ \lim\limits_{x \to 0+0}3x =3*(0+0)=3*0=0.\\f(0)=3*0=0.\ \ \ \ \ \Rightarrow\\$

x₀=0 - это точка непрерывности.

$x_0=2.\\ \lim_{x \to 2-0} 3x=3*(2-0)=3*2=6.\\ \lim\limits_{x \to 2+0} (3-x) =3-2-0=1.\\f(2)=3-2=1.\ \ \ \ \ \Rightarrow\\$

x₀=2 - это точка разрыва первого рода.

Приложения:

sangers1959: Я решаю дальше.

sangers1959: Решил.

cychvj: можете помочь задача по технической механике пожалуйста

cychvj: где можно с вами связаться

Аноним: спасибо большое, если будете свабодны помогите еще

Похожие вопросы

Английский язык

1 год назад

HOW MANY ...HAS SHE GOT?

Английский язык

1 год назад

Плиз помогите Характеристика фильма Ривирдэйл на английском языке

Русский язык

2 года назад

Помогите составить предложение со словом обут

Русский язык

2 года назад

1) 10 причастий с 1-ой н 2) 10 причастий с 2-мя н 3) 10 отглагольных прилагательных с 1-ой н 4)10 отглагольных прилагательных с 2-мя н

Литература

7 лет назад

краткий отзыв М.Пришвин ,,кладовая солнца,

Математика

7 лет назад

Найдите наибольший общий делитель и наименьшее общее кратное чисел:3*5в квадрате*7в квадрате и 2в кубе*5*7

История

9 лет назад

кто управлял нестяжателями

Математика

9 лет назад

помогите пожалуйста решить