Ответы
Ответ дал:
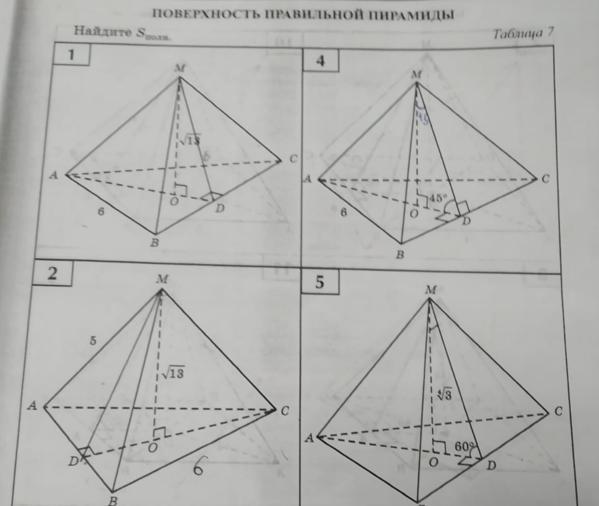
1
Ответ:
9√3+9√6 ед²
Решение:
S(∆ABC)=AB²√3/4=6²√3/4=
=9√3 ед² площадь основания.
OD- радиус вписанной окружности.
r=a/2√3;, где а-сторона треугольника.
ОD=6/2√3=√3 ед.
∆МОD- прямоугольный, равнобедренный треугольник. OD=MO=√3
По теореме Пифагора
MD=√(OD²+MO²)=
=√((√3)²+(√3)²)=√(3+3)=√6 ед.
Sбок=½*МD*BC*3=½*6*√6*3=
=9√6ед²
Sпол=Sбок+Sосн=
=9√3+9√6 ед²
9√3+9√6 ед²
Решение:
S(∆ABC)=AB²√3/4=6²√3/4=
=9√3 ед² площадь основания.
OD- радиус вписанной окружности.
r=a/2√3;, где а-сторона треугольника.
ОD=6/2√3=√3 ед.
∆МОD- прямоугольный, равнобедренный треугольник. OD=MO=√3
По теореме Пифагора
MD=√(OD²+MO²)=
=√((√3)²+(√3)²)=√(3+3)=√6 ед.
Sбок=½*МD*BC*3=½*6*√6*3=
=9√6ед²
Sпол=Sбок+Sосн=
=9√3+9√6 ед²
Похожие вопросы
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад