СРОЧНОООООО




В окружность вписан треугольник, причём центр окружности оказался внутри этого треугольника. Доказать, что данный треугольник остроугольный.

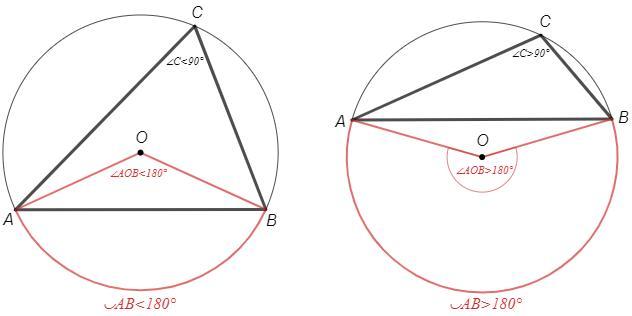
Пусть центр описанной окружности (O) внутри треугольника. Соединим его с вершинами. Получим центральные углы (AOB, BOC, AOC) меньше 180° и дуги (AB, BC, AC) меньше 180°. Тогда вписанные углы (A, B, C), опирающиеся на эти дуги, меньше 90° (вписанный угол равен половине дуги, на которую опирается).