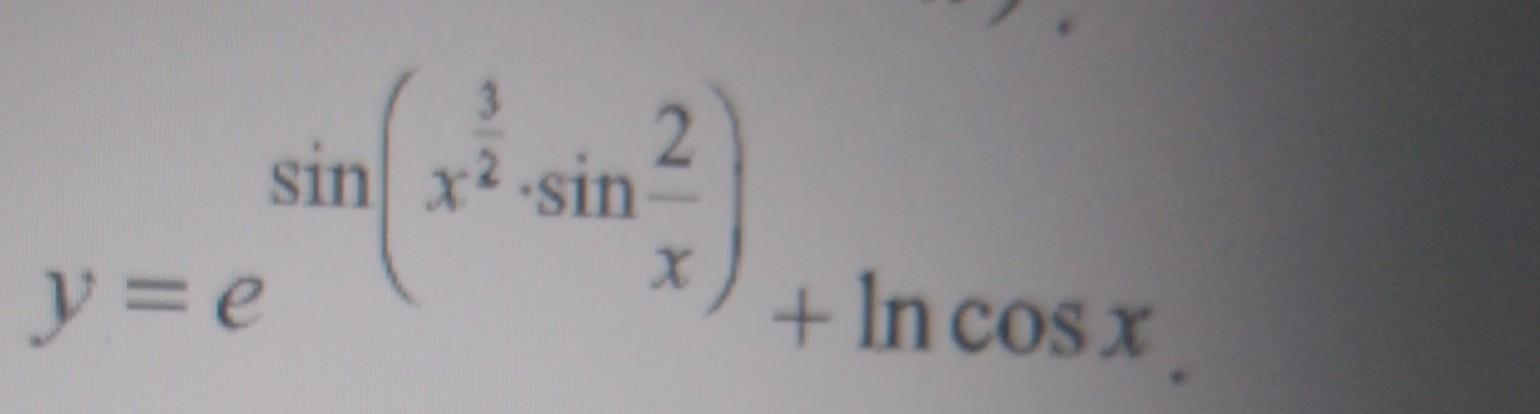70 БАЛОВ
найти y' по даному уровнение​

Ответ:

(1/(e^(x²/³sin2/x)+㏑cosx)*((e^(x²/³sin2/x)*cos(x²/³sin2/x)*((3/2)*∛x*sin(2/x)+x³/²*cos(2/x)*-(2/x²))-tgx))

Пошаговое объяснение:

㏑(e^(x²/³sin2/x)+㏑cosx)

y'/y=(1/(e^(x²/³sin2/x)+㏑cosx)*((e^(x²/³sin2/x)*cos(x²/³sin2/x)*((3/2)*∛x*sin(2/x)+x³/²*cos(2/x)*-(2/x²))+(-sinx/cosx))=

(1/(e^(x²/³sin2/x)+㏑cosx)*((e^(x²/³sin2/x)*cos(x²/³sin2/x)*((3/2)*∛x*sin(2/x)+x³/²*cos(2/x)*-(2/x²))-tgx))