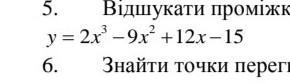Ответы
Ответ дал:
3
Сперва найдём производную.
Найдём нули производной.
Определим знаки производной на промежутках.
x<1 - производная положительна.
1<x<2 - производная отрицательна.
x>2 - производная положительна.
Значит при х<1 и x>2 функция возрастает, а при 1<x<2 убывает.
Похожие вопросы
1 год назад
2 года назад
7 лет назад
7 лет назад
9 лет назад