Дан правильный треугольник АВС. На продолжении стороны АС за точку С взята точка Д, а на продолжении стороны ВС за точку С - точка Е так, что ВД=ДЕ. Известно, что АД=5. Найдите СЕ.​

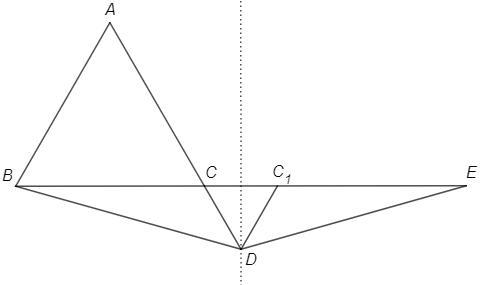
Равнобедренный треугольник (BDE) симметричен относительно серединного перпендикуляра к основанию (BE).

Возьмем точку С1, симметричную С относительно серединного перпендикуляра к BE.

C1D=CD, C1E=BC

△CDC1 - р/б с углом 60° - равносторонний, CD=CC1

AD =AC+CD =C1E+CC1 =CE

Или

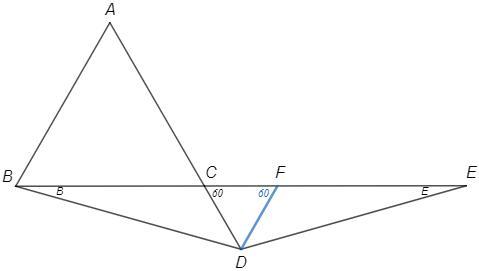
Пусть DF||BA

△DFC~△ABC (стороны параллельны) => △DFC -равносторонний

∠BDC =60°-∠B =60°-∠E =∠EDF

△BDC=△EDF (по стороне и прилежащим углам) => BC=EF

AD =AC+CD =BC+CF =EF+CF =CE