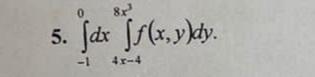Предмет: Математика
Автор: bibidoskali
Вопрос задан 6 лет назад

Изменить порядок интегрирования в двойном интеграле.

Приложения:

Ответы

Ответ дал: Alnadya

Решение.

$\displaystyle \int\limits_{-1}^0\, dx \int\limits_{4x-4}^{8x^3}f(x,y)\, dy$

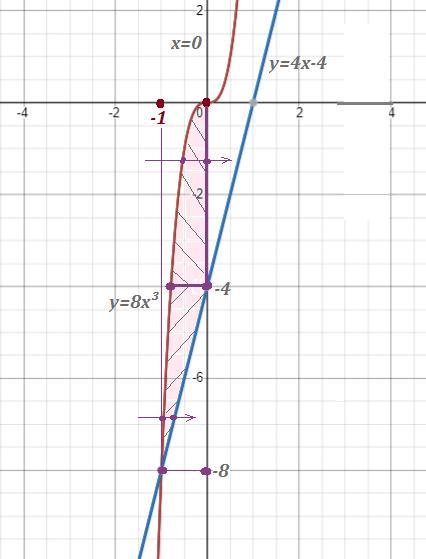
Область нарисована на чертеже. Чтобы изменить порядок интегрирования, надо спроецировать эту область на ось ОУ . Тогда мы видим, что область можно разбить на 2 части.

Одна проецируется в отрезок от -8 до -4 . Точка входа в эту область лежит на кубической параболе у=8х³ ⇒ $x=\sqrt[3]{\dfrac{y}{8}}$ , точка выхода лежит на прямой у=4х-4 ⇒ х=(y/4)+1 .

Вторая область проецируется в отрезок от -4 до 0 . Точка входа лежит на кубической параболе у=8х³ ⇒ х=∛(у/8) , точка выхода лежит на прямой х=0 .

$\displaystyle \int\limits_{-1}^0\, dx \int\limits_{4x-4}^{8x^3}f(x,y)\, dy=\displaystyle \int\limits_{-8}^{-4}\, dy \int\limits^{\frac{y}{4} +1}_{\sqrt[3]{\frac{y}{8}}}f(x,y)\, dx+\displaystyle \int\limits_{-4}^0\, dy \int\limits_{8x^3}^0\, f(x,y)\, dx$