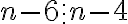Ответы
Ответ дал:
2
Так как n - натуральные числа, то n≥1.
n не может быть нечётным числом, иначе оно никогда не будет делиться на нечётное число без остатка при данных условиях.
При n≥7 число (n-6) никогда не будет делиться на число (n-4), так как одно из чисел меньше другого по модулю.
Остается рассмотреть варианты при n=2, n=4 и n=6.
При n=2: (-4):(-2)=2 - подходит.
При n=4: (-2):(0) - невозможно, т.к. делить на ноль нельзя.
При n=6: (0):(-2)=0 - подходит.
Значит сумма всех натуральных n будет равна 2+6=8.
Ответ: 8.
n не может быть нечётным числом, иначе оно никогда не будет делиться на нечётное число без остатка при данных условиях.
При n≥7 число (n-6) никогда не будет делиться на число (n-4), так как одно из чисел меньше другого по модулю.
Остается рассмотреть варианты при n=2, n=4 и n=6.
При n=2: (-4):(-2)=2 - подходит.
При n=4: (-2):(0) - невозможно, т.к. делить на ноль нельзя.
При n=6: (0):(-2)=0 - подходит.
Значит сумма всех натуральных n будет равна 2+6=8.
Ответ: 8.
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
8 лет назад