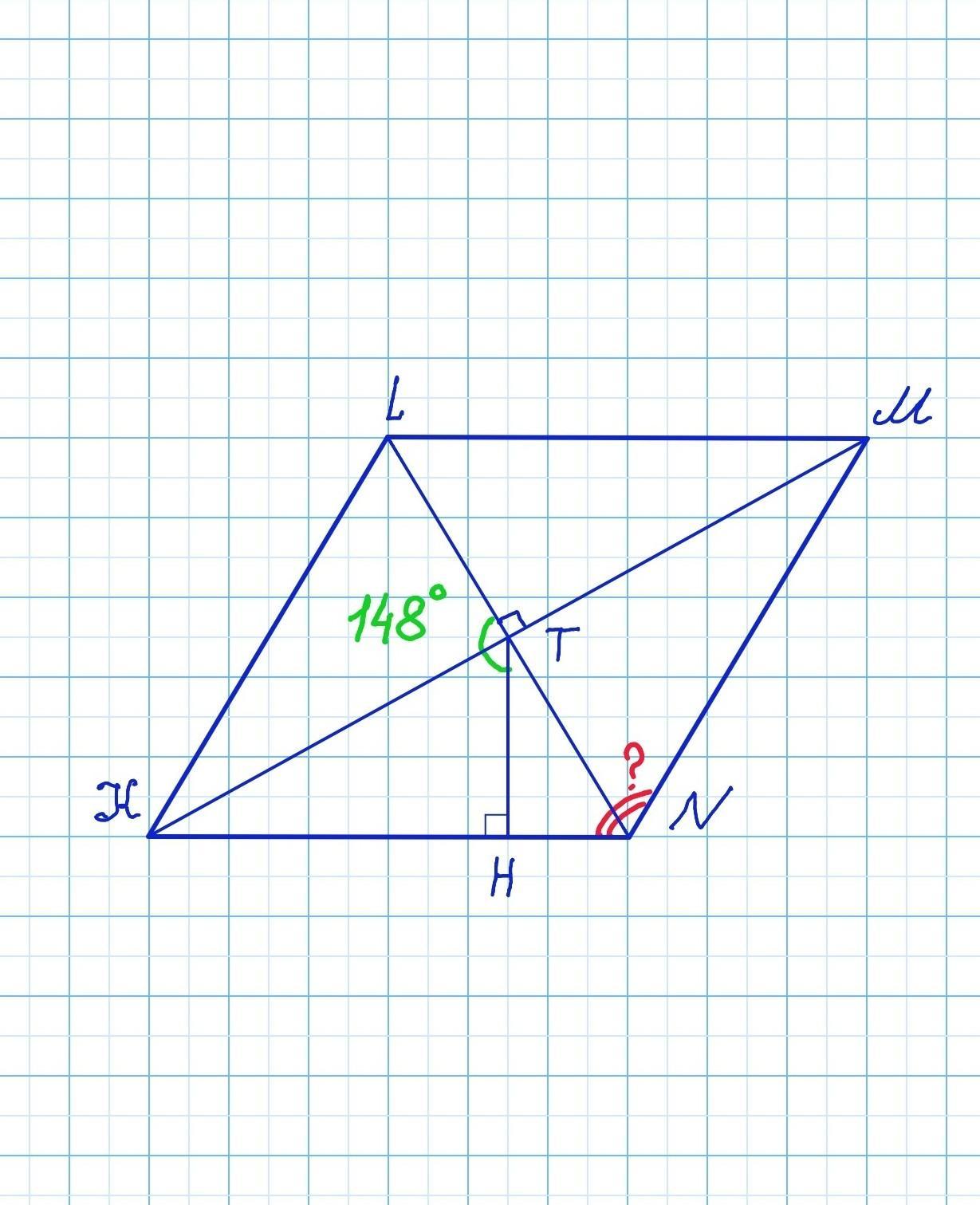
В ромбе KLMN диагонали пересекаются в точке T. Из точки T опущен перпендикуляр TH на сторону KN. Найдите тупой угол ромба, если ∠LTH = 148°. Ответ дайте в градусах.

Ответ:

Тупой угол ромба равен 116°.

Пошаговое объяснение:

Дано: Ромб KLMN. Диагонали ромба KLMN пересекаются в точке Т. ТН⟂ KN. ∠LTH = 148°.

Найти: ∠KNM.

∠HTN=∠LTN-∠LTH=180°-148°=32°.

Так как ТН⟂ KN, то △ТНN - прямоугольный (∠H=90).

Сумма острых углов прямоугольного треугольника равна 90°, следовательно

∠TNH=90°-∠HTN=90°-32°=58°.

Диагонали ромба являются биссектрисами его углов. Следовательно ∠KNM=2×∠TNH=2×58°=116°.

Так как 116°>90°, то ∠KNM - тупой, а значит искомый.