Известно, что стороны, прилегающие к прямому углу треугольника, относятся как 2 : 5, а их разность равна 1/5. Найдите площадь этого треугольника.
Пожалуйста помогите!!!!!!
Ответы
Ответ дал:
25
Ответ:
1/45
Объяснение:
Дан треугольник АВС (∠С=90°),
ВС/АС=2/5
АС-ВС=1/5
SΔАВС=?
пусть коэффициент пропорциональности х, тогда АС=5х, ВС=2х
согласно условия 5х-2х=1/5
умножим обе части уравнения на 5,
25х-10х=1
15х=1
х=1/15
площадь треугольника АВС: SΔАВС=0.5АС*ВС=0.5*5х*2х=5х²
SΔАВС=5*(1/15)²=5/225=1/45
Приложения:
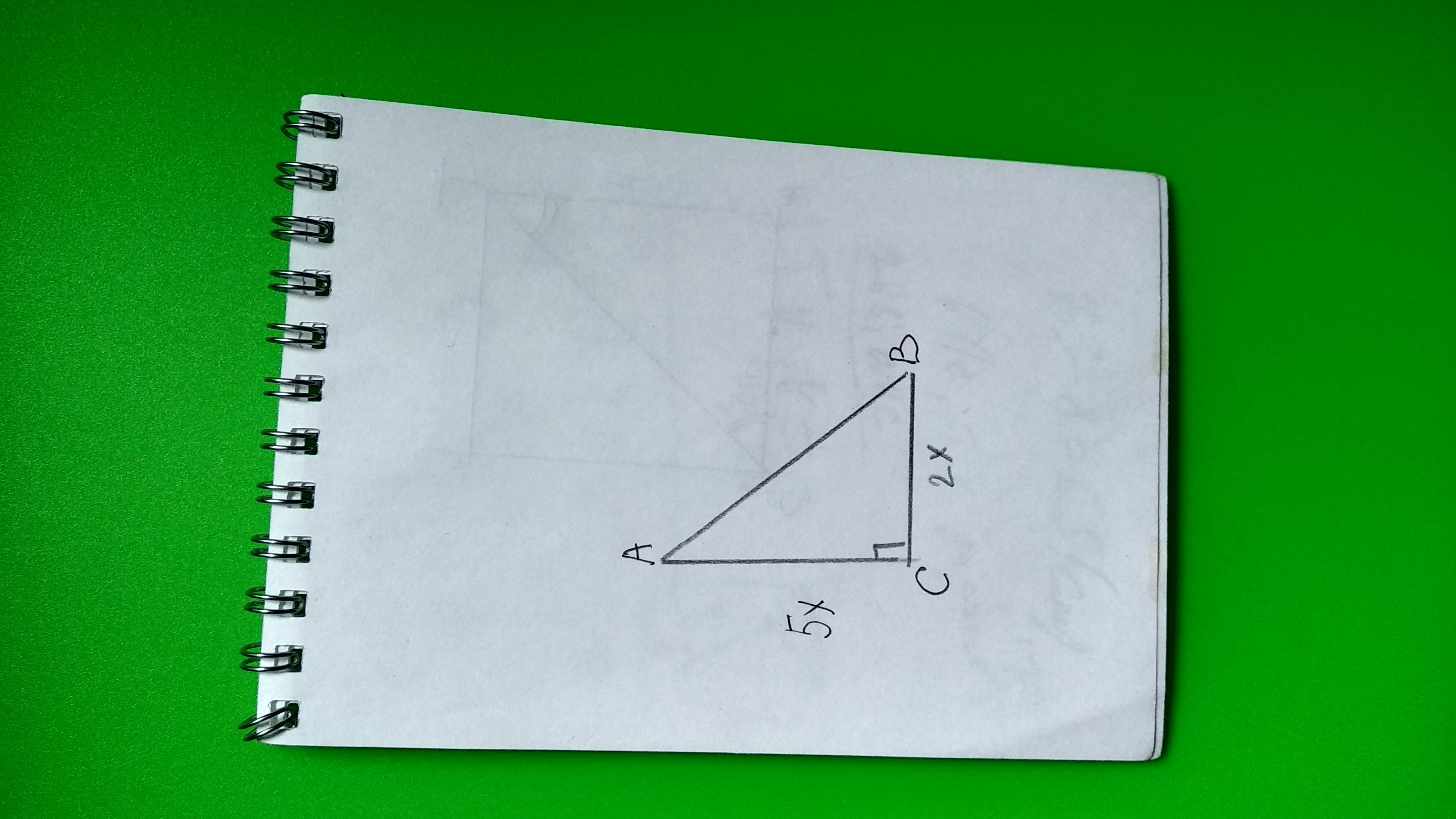
Polichyk037:
/ - это делить?
это обозначает дробь
а откуда ты взял 25х, 10х, 0.5?
да. это делВС/АС=2/5
АС/ВС=1/5
SΔАВС=?
пусть коэффициент пропорциональности х, тогда АС=5х, ВС=2х
согласно условия 5х-2х=1/5
25х-10х=1
15х=1
х=1/15
площадь треугольника АВС: SΔАВС=0.5АС*ВС=0.5*5х*2х=5х²
SΔАВС=5*(1/5)²=1/5ение. а
АС/ВС=1/5
SΔАВС=?
пусть коэффициент пропорциональности х, тогда АС=5х, ВС=2х
согласно условия 5х-2х=1/5
25х-10х=1
15х=1
х=1/15
площадь треугольника АВС: SΔАВС=0.5АС*ВС=0.5*5х*2х=5х²
SΔАВС=5*(1/5)²=1/5ение. а
а откуда 0.5?
по формуле площади
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад