100 баллов ! Высота правильной четырехугольной пирамиды равна 12 см, а боковое ребро

4 см. Найдите угол между основанием пирамиды и плоскостью сечения, проходящего через сторону основания и середину скрещивающегося с ним бокового ребра

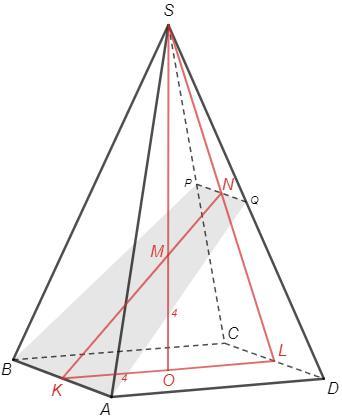
Правильная четырехугольная пирамида

- в основании квадрат

- вершина падает в центр основания (O)

Пусть P - середина SC

PQ - след сечения в грани SCD

CD||AB, грань SCD параллельна AB

PQ не пересекается с AB и лежит с ней в одной плоскости => PQ||AB

K, L - середины ребер AB и CD

Рассмотрим SKL

KL⊥AB => MK⊥AB (т о трех перпендикулярах)

∠MKO - искомый угол

N - середина SL (т Фалеса, PQ||AB)

M - точка пересечения медиан, MO =1/3 SO =12/3 =4

AO =√( (4√11)^2 -12^2 ) =4√2 (△SAO, т Пифагора)

KO =AO/√2 =4

tg(MKO) =MO/KO =1 => ∠MKO=45°