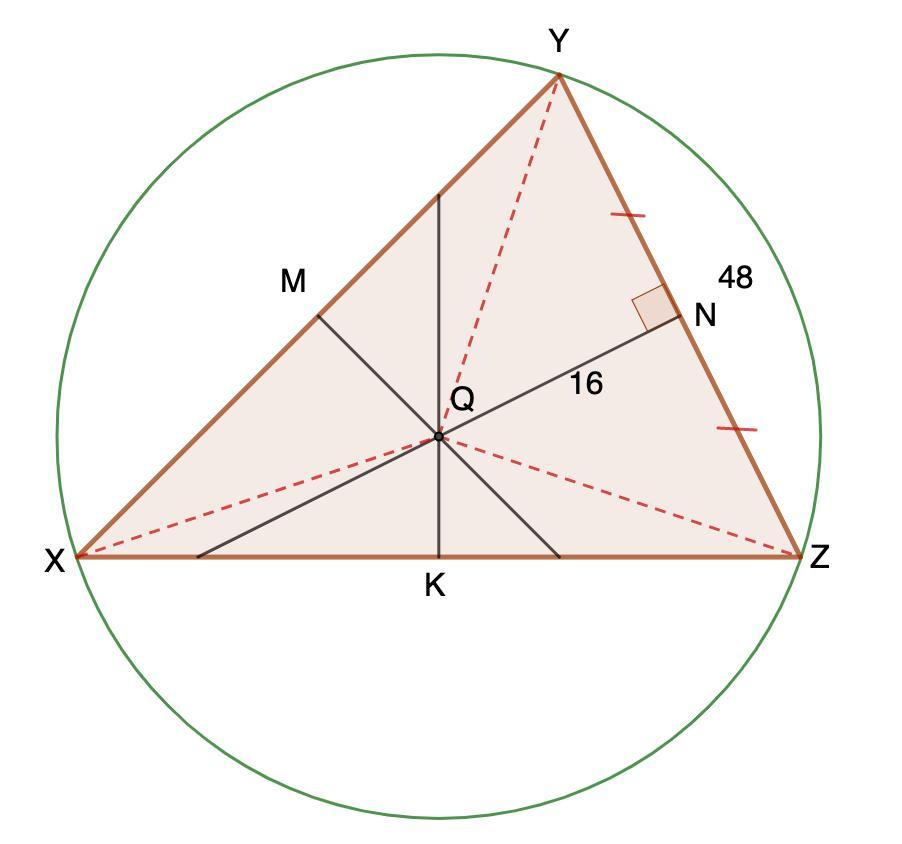
В остроугольном треугольнике XYZ серединные перпендикуляры пересекаются в точке Q . Точки M , N , K являются основаниями серединных перпендикуляров на сторонах XY , YZ и ZX соответственно. Определи величину XQ , если QN=16 , а YZ = 48.
Помогите пожалуйста

Ответ:

Величина XQ равна 8√13 ед.

Объяснение:

Определить величину XQ.

Дано: ΔXYZ;

M, N, K - основания серединных перпендикуляров;

M ∈ XY; N ∈ YZ; K ∈ ZX;

QN = 16; YZ = 48.

Найти: XQ.

Решение:

• Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

⇒ Q - центр описанной окружности около ΔXYZ.

⇒ QX = QY = QZ - радиусы описанной окружности.

Рассмотрим ΔQYN - прямоугольный.

ZN = NY = 48 : 2 = 24 (QN - серединный перпендикуляр)

По теореме Пифагора найдем QY:

QY² = QN² + NY² = 256 + 576 = 832

QY = √832 = 8√13

⇒  QX = QY = QZ = 8√13 (ед.)

Величина XQ равна 8√13 ед.

#SPJ1