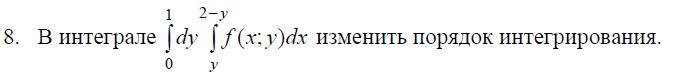Предмет: Алгебра
Автор: Reideen
Вопрос задан 6 лет назад

Задание приложено...

Приложения:

Ответы

Ответ дал: mathkot

Ответ:

$\boxed{ \boldsymbol{ \displaystyle \int\limits^{1}_{0} \, dy \int\limits^{2 - y}_{y} {f(x,y)} \, dx = \int\limits^{1}_{0} \, dx \int\limits^{x}_{0} {f(x,y)} \, dy + \int\limits^{2}_{1} \, dx \int\limits^{2 -x}_{0} {f(x,y)} \, dy } }$

Объяснение:

$\displaystyle \int\limits^{1}_{0} \, dy \int\limits^{2 - y}_{y} {f(x,y)} \, dx$ - интегрирование происходит по $y$ , так как первый интеграл интегрируется по $dy$ .

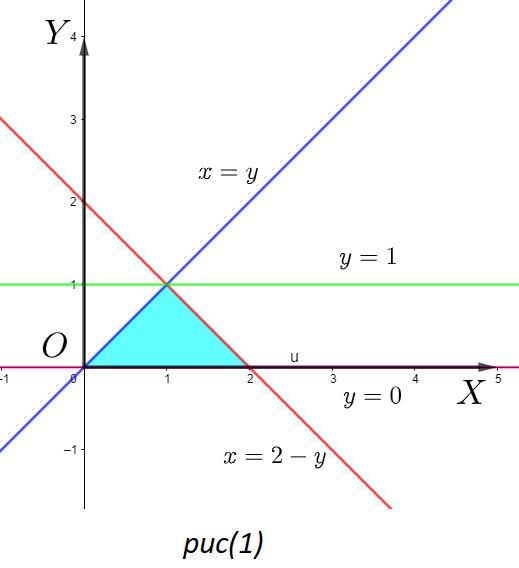
Построим область интегрирования (рис(1)) по y:

$x = y; y = x$

$x = 2 - y; y = 2- x$

$y = 0$

$y = 1$

При интегрировании по x нужно записать функции обратные тем, которые были при интегрировании по y, то есть:

$y = x;$

$y = 2 - x$

Пересечения с прямой $y = 0:$

$y = x;$ в точке (0;0)

$y =2- x;$ в точке (2;0)

Пересечения с прямой $y = 1:$

$y = x;$ в точке (1;1)

$y =2- x;$ в точке (1;1)

Найдем абсциссу пересечения графиков $y = x$ и $y = 2 - x$

$x = 2- x$

$2x = 2|:2$

$x = 1$

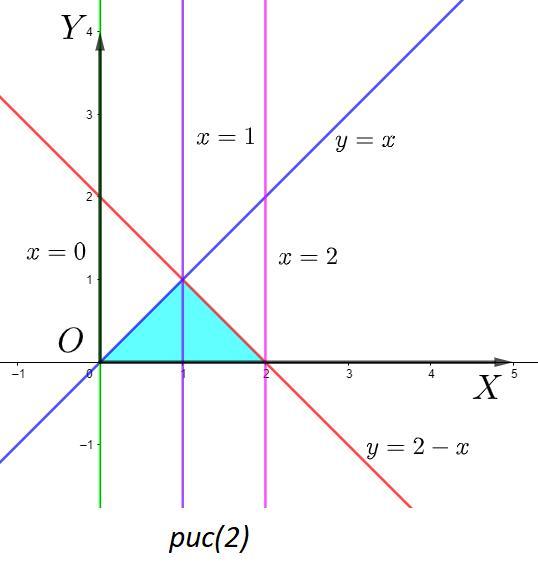
Построим область интегрирования (рис(2)) по x:

$y = x;$

$y = 2 - x;$

$x = 0;$

$x = 1;$

$x = 2;$

$\displaystyle \int\limits^{1}_{0} \, dy \int\limits^{2 - y}_{y} {f(x,y)} \, dx = \int\limits^{1}_{0} \, dx \int\limits^{x}_{0} {f(x,y)} \, dy + \int\limits^{2}_{1} \, dx \int\limits^{2 -x}_{0} {f(x,y)} \, dy$