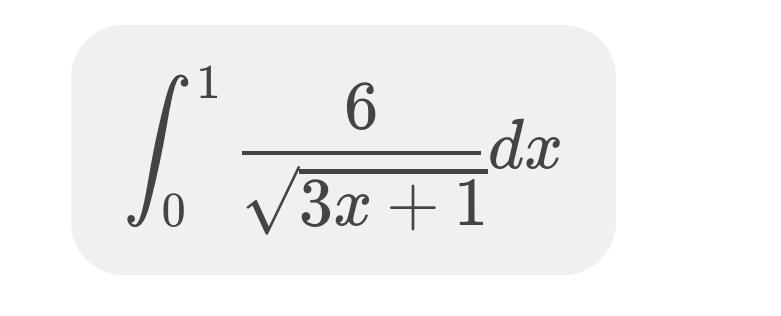Вычислить интеграл, желательно подробно
Пример необходимого типа решения на 2 фото

Ответ:

Пошаговое объяснение:

Сделаем замену:

t = √ (3x + 1)

t² = 3x + 1

3x = t² - 1

x = (t² - 1) / 3

dx = (2/3)·t ·dt

Изменим пределы интегрирования:

При x = 0;     t = 1

При x = 1;     t = 2

Подыниегральное выражение:

6·dx / √ (3x+1) = 6·(2/3)·t·dt / t = 4·dt

И тогда :