СРОЧНО РЕШИТЕ ПОЖАЛУЙСТА


ДАМ 60 БАЛЛОВ​

Ответ:
МА=2√3
P(∆MNK)=12
S(∆MNK)=6

Решение:
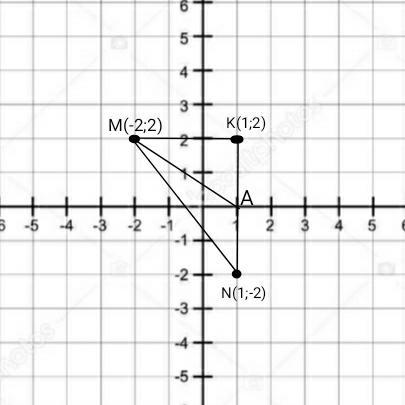
А(Ха;Уа)
т.А середина отрезка КN
Xa=(Xк+Xn)/2=(1+1)/2=1
Уа=(Ук+Уn)/2=(2-2)/2=0
A(1;0)
MA=√((Xa-Xм)²+(Уа-Ум)²)=
=√((1-(-2))²+(0-2)²)=
=√((1+2)²+(-2)²)=√(3²+4)=
=√12=2√3.

МК=|Xм|+|Хк| =|-2|+|1|=3
КN=|Ук|+|Уn|=|2|+|-2|=4
Треугольник прямоугольный.
По теореме Пифагора
МN=√(MK²+KN²)=√(3²+4²)=5
P(∆MNK)=MN+MK+KN=3+4+5=
=12

S(∆MNK)=MK*KN/2=3*4/2=6