СРОЧНО Доведіть,що вираз x²-10x+29 набуває лише доданих значень при всіх значеннях змінної x.

Решение.

Квадратный трёхчлен    со старшим коэффициентом  

а=1>0 принимает только положительные значения лишь в случае,

когда его дискриминант D<0 .

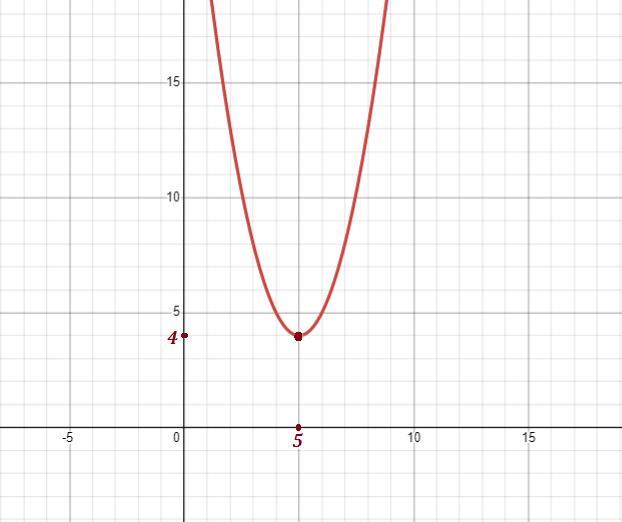
График такой параболы не пересекается с осью Ох и находится выше оси Ох

Доказано .

Объяснение: