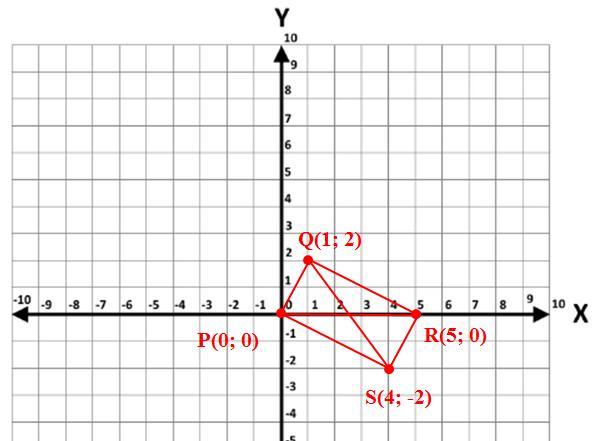
вершинами четырехугольника PQRS являются точки P(0;0) Q(1;2) R(5;0) и S(4;-2). Докажите , что данный четырехугольник является прямоугольником. ПОМОГИТЕ СПОЧНО ПЖ!!

Ответы

Ответ дал: axatar

Ответ:

Доказательство в объяснении

Объяснение:

Один из способов доказательств:

1) Докажем, что несмежные стороны четырёхугольника равны;

2) Докажем, что диагонали четырёхугольника равны.

Отсюда следует, что четырёхугольник является прямоугольником.

Нужно знать:

Расстояние между точками M(x₁; y₁) и N(x₂; y₂) вычисляется по формуле:

$\displaystyle \tt d(MN)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} .$

Решение. Вычислим длины сторон и диагоналей четырёхугольника (см. рисунок):

$\displaystyle \tt d(PQ)=\sqrt{(0-1)^2+(0-2)^2} =\sqrt{1^2+2^2} =\sqrt{1+4} =\sqrt{5} ;$

$\displaystyle \tt d(RS)=\sqrt{(5-4)^2+(0-(-2))^2} =\sqrt{1^2+2^2} =\sqrt{1+4} =\sqrt{5} ;$

$\displaystyle \tt d(QR)=\sqrt{(1-5)^2+(2-0)^2} =\sqrt{4^2+2^2} =\sqrt{16+4} =\sqrt{20} ;$

$\displaystyle \tt d(SP)=\sqrt{(4-0)^2+(-2-0)^2} =\sqrt{4^2+2^2} =\sqrt{16+4} =\sqrt{20} ;$

$\displaystyle \tt d(PR)=\sqrt{(0-5)^2+(0-0)^2} =\sqrt{5^2+0^2} =\sqrt{25} =5;$

$\displaystyle \tt d(QS)=\sqrt{(1-4)^2+(2-(-2))^2} =\sqrt{3^2+4^2} =\sqrt{9+16} =\sqrt{25}=5 ;$

Так как d(PQ)=d(RS), d(QR)=d(SP) и d(PR)=d(QS), то несмежные стороны четырёхугольника равны и равны диагонали.

Значит, четырёхугольник является прямоугольником.

#SPJ1

Приложения:

Похожие вопросы

Окружающий мир

1 год назад

Русский язык

1 год назад

Русский язык

2 года назад

Русский язык

2 года назад

Математика

7 лет назад

Биология

7 лет назад

Химия

9 лет назад

Математика

9 лет назад