СРОЧНО!!!Даю 30 баллов условие читайте внимательно
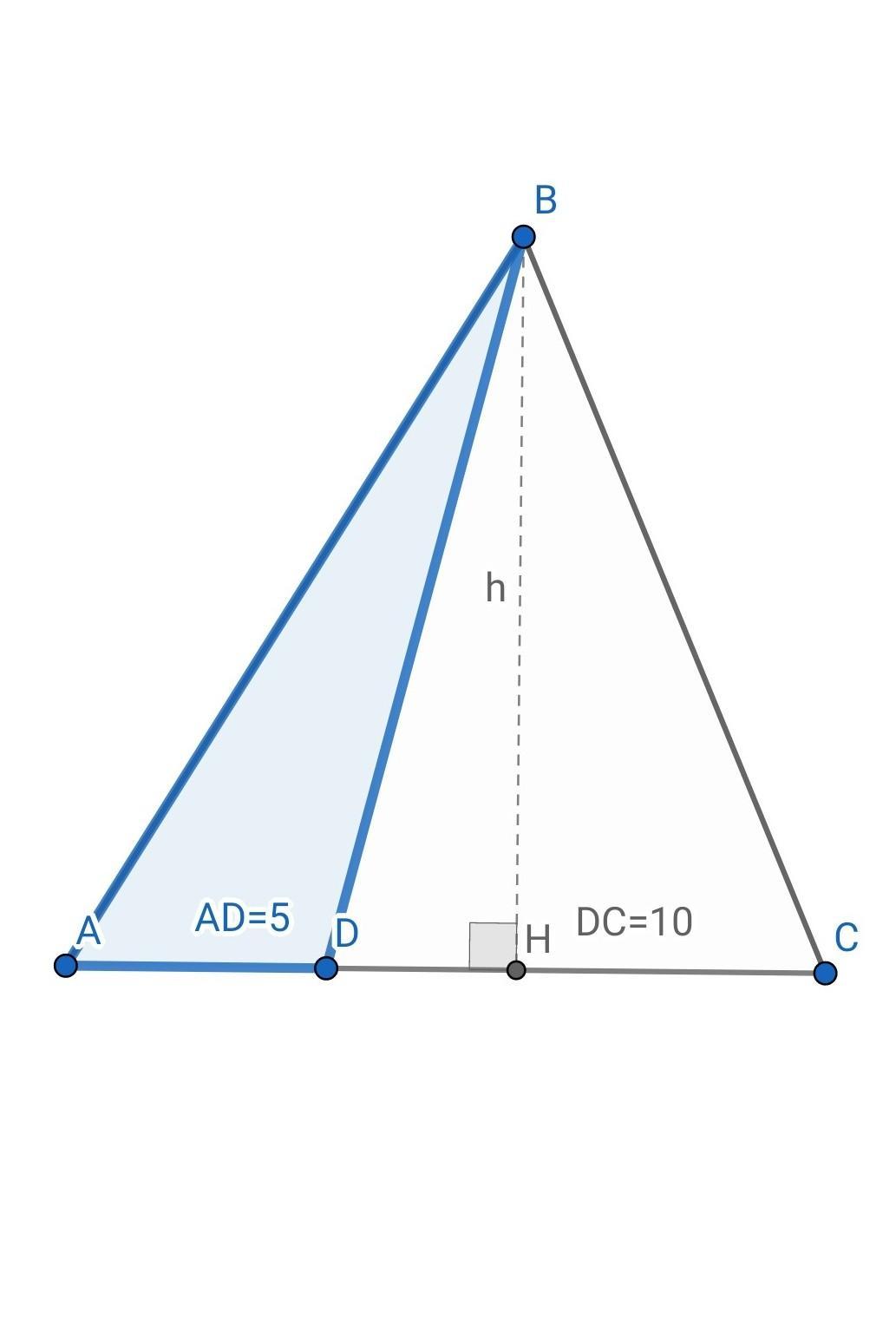
На стороне AC треугольника ABC отмечена точка D так, что AD = 5, DC = 10. Площадь треугольника ABC равна 60 см². Найдите площадь треугольника ABD.

Ось розв'язок !

тримайте на здоров'я.

Ответ:

Объяснение:

Дано:

Найти:

Решение

Т.к. D принадлежит АС, найдем длину отрезка АС:

Выпазим площадь ∆ как половину произведения стороны на опущенную к ней высоту.

Проведем в ∆АВС высоту ВН; ВН _|_ АС

Но так как

То есть для обоих треугольников высота - одна и та же, обозначим её как h

Тогда получаем для ∆АВС

А для ∆ABD

Следовательно

А значит