Будь ласка, допоможіть!!!Потрібно сьогодні!!! Знайдіть проміжки зростання, спадання і точки екстремуму фукнції f(x)=x^4+2x^3. Зразу дякую <3

Ответ:

1)  x₁ = 0;  x₂ = -1.5    - критические точки

2)  точка x₂ = 1,5 - точка минимума.

3)

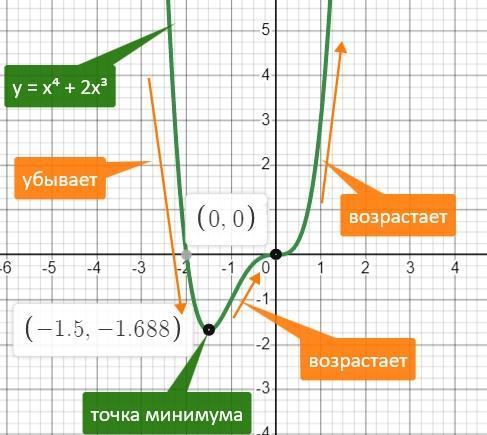
(-∞; -1,5)    функция убывает

(-1,5; 0)      функция возрастает

(0; +∞)        функция возрастает

Объяснение:

у = x⁴ + 2x³

Первая производная

y' = 4x³ + 6x² = 2x²( 2x + 3)

2x²( 2x + 3) = 0;     x₁ = 0;  x₂ = -1.5    - критические точки

Рассмотрим поведение производной на промежутках

(-∞; -1,5)     у'(-2) = -4   < 0     функция убывает

(-1,5; 0)      у'(-1) = 2      > 0    функция возрастает

(0; +∞)         у'(1) = 10     > 0    функция возрастает

В окрестности точки x₂ = -1,5 производная функции меняет знак с (-) на (+). Следовательно, точка x₂ = 1,5 - точка минимума.