Доведіть, що многочлен, тотожно рівний виразу (x-4)^2n + (x-3)^n - 1, де n є N(натуральним), ділиться націло на многочлен x^2 - 7x + 12.
Приложения:
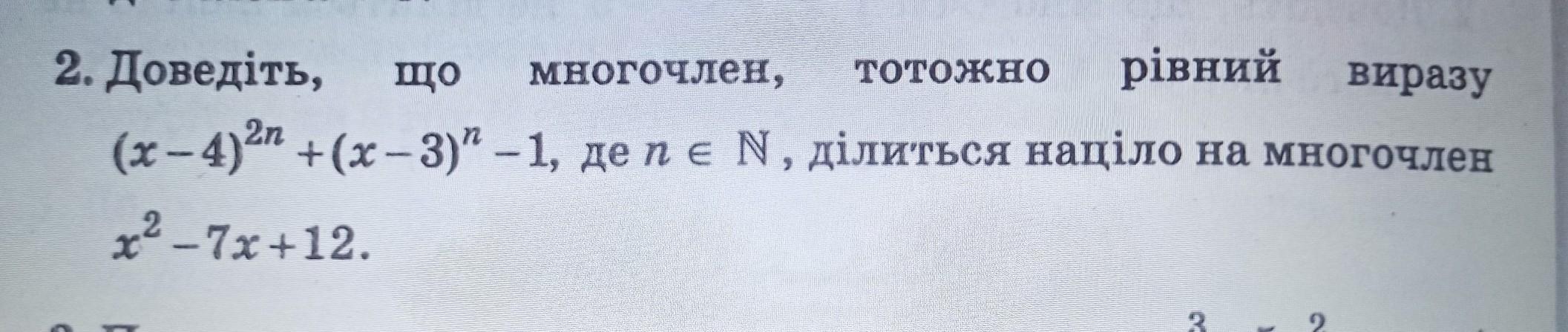
XxDayDreemerxX:
hi
hi
wanna talk I m bored
sorry man but i do my homework now
ok ):< it's fine
Ответы
Ответ дал:
1
Ответ:
Объяснение:
если многочлен f(x)=(x-4)²ⁿ+(x-3)ⁿ-1 делится без остатка на многочлен g(x)=x²-7x+12, то корни многочлена g(x) являются и корнями многочлена f(x)
x²-7x+12=0⇒x₁=4, x₂=3 (по теореме Виета)
f(4)=(4-4)²ⁿ+(4-3)ⁿ-1=0²ⁿ+1ⁿ-1=0+1-1=0
f(3)=(3-4)²ⁿ+(3-3)ⁿ-1=(-1)²ⁿ+0ⁿ-1=1+0-1=0
все!
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад