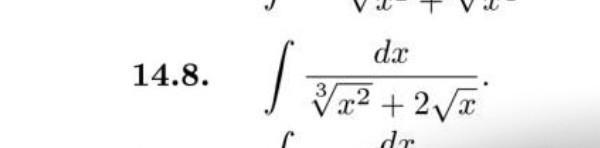Предмет: Алгебра
Автор: Аноним
Вопрос задан 6 лет назад

< >

помогите пожалуйста решить задачу

Приложения:

Ответы

Ответ дал: NNNLLL54

0

Ответ:

Замена переменной в неопределённом интеграле .

$\displaystyle \int \frac{dx}{\sqrt[3]{x^2}+2\sqrt{x}}=\Big[\ x=t^6\ ,\ dx=6\, t^5\, dt\ \Big]=\int \frac{6\, t^5\, dt}{\sqrt[3]{t^{12}}+\sqrt{t^6}}=6\int \frac{t^5\, dt}{t^4+t^3}=\\\\\\=6\int \frac{t^2\, dt}{t+1}=6\int \Big(t-1+\frac{1}{t+1}\Big)\, dt=6\cdot \Big(\frac{t^2}{2}-t+ln|\, t+1\, |+C_1\Big)=\\\\\\=3\sqrt[3]{x}-6\sqrt[6]{x}+6\, ln|\, \sqrt[6]{x}+1\, |+C$

Аноним: спасибо большое

Аноним: и еще один остался вопрос помогите пожалуйста

Похожие вопросы

Русский язык

1 год назад

Ребята помогите мне! Сочинение на тему :《 Почему мы должны помнить?》 (имеется виду зачем нужно помнить про вов,героев и ветеранов? минимум 2 аргумента ) С ОБЪЁМОМ 170 СЛОВ! Заранее большое спасибо.

Русский язык

1 год назад

Помогите пожалуйста срочно.4 и 5.спасибо. нужен пересказ и изложение.спасибо.

Русский язык

2 года назад

Подбери проверочные слова.Все ли безударные гласные можно проверить. Образеть:золотить-золото,позолота. (голосистый,молоко, молодой,городской,сторожить,сторона.)

Русский язык

2 года назад

Придумай и запишите шесть предложений с одним из данных слов так , чтобы выбранное вами слово употреблялось во всех шести падежах по порядку . В записанных предложениях укажите . к какой части речи

Математика

7 лет назад

Задача. Первый человек идет со скоростю 6км/час , доганяет второго,который идет со скоростю 4 км/час. Через сколько часов первый человек догонит второго, если с начала между ними было растояние 10 км

Алгебра

7 лет назад

Помогите/// 7 класс, алгебра

Физика

9 лет назад

Сколько α и β распадов происходит в результате превращения Палладия 226 на Плюмбум 206

Биология

9 лет назад

кислород при фотосинтезе образуется в процессе : 1) темновой фазы 2)расщепления воды 3) образования глюкозы 4)усвоения углекислого газа .