алгебра еще система уравнений СРОЧНО. Просьба добавлять ответ, только если знаете. Я ЗАКОЛЕБАЛСЯ УДАЛЯТЬ ОТВЕТІ ИНДИВИДУМОВ, КОТОРІЕ НЕ ЗНАЮТ ОТВЕТ И ПРОСТО СПАМЯТ!!!!!

Приложения:

Пеппер: это не система уравнений, вопрос неправильный

Barabanen228: Это система неравенств с параметром

Ответы

Ответ дал: axatar

Ответ:

При a = 6

Объяснение:

Перевод: При каком наименьшем целом значении а система неравенств имеет хотя бы одно решение:

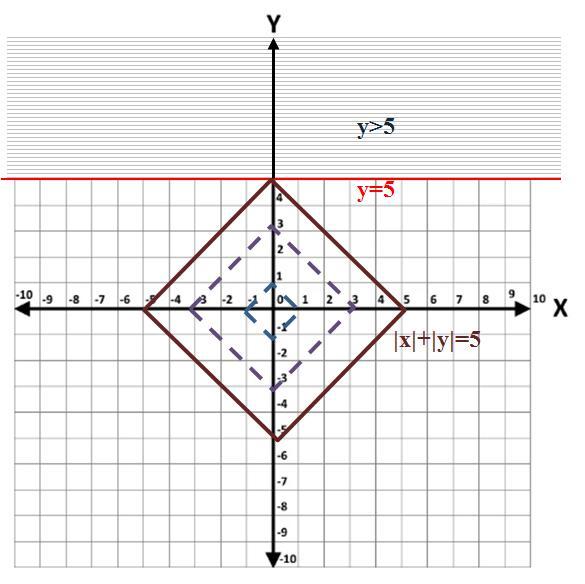
$\displaystyle \left \{ {{|x|+|y| \leq a} \atop {y > 5}} \right. .$

Решение. Множество, для для которого выполняется неравенство y>5, это часть плоскости (на рисунке заштрихованная часть плоскости кроме красной границы), ограниченной снизу прямой y=5 (на рисунке красная линия).

Множество, для для которого выполняется неравенство |x|+|y|≤a, это часть плоскости (на рисунке ромбики (как примеры при а=1, 3 и 5), ограничивающие часть плоскости, содержащую начало координат).

Система означает пересечение обоих множеств. Отсюда, система имеет решение если a>5.

По условию нам нужно определить наименьшее целое значение а: это 6.

#SPJ1

Приложения: