Здравствуйте. Пожалуйста помогите решить задачу.
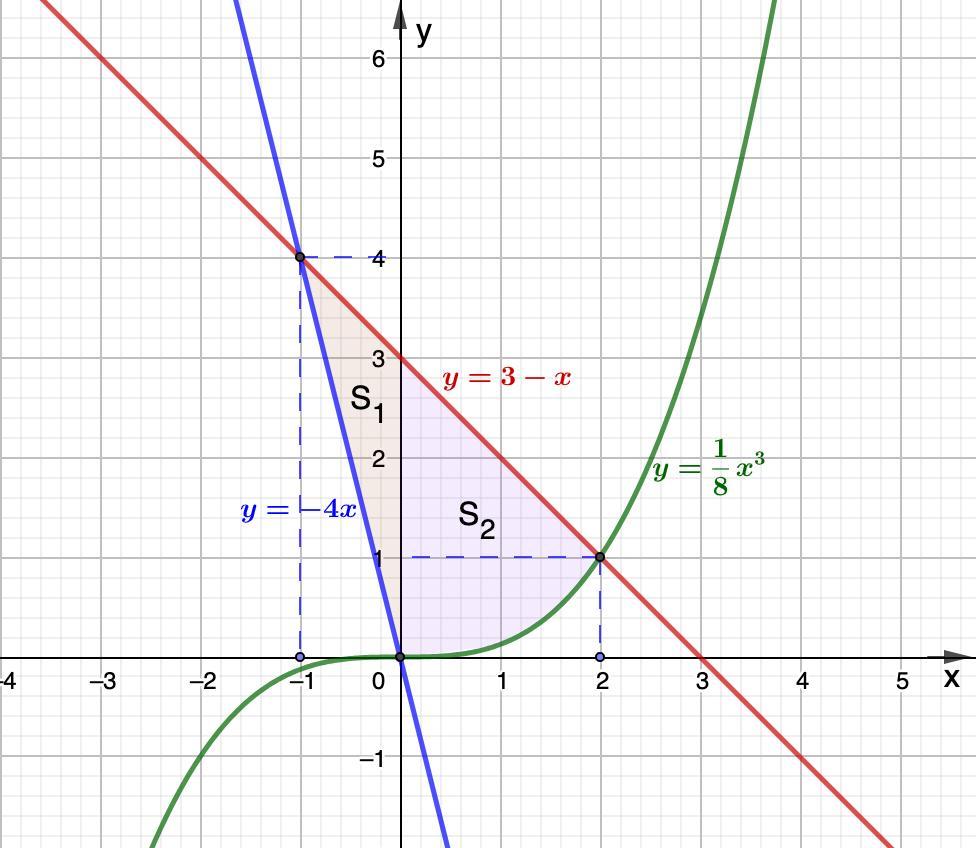
Вычислите площадь фигуры, ограниченной заданными линиями: y=1/8×x^3, y=3-x, y = - 4x.

Ответы

Ответ дал: natalyabryukhova

Ответ:

Площадь фигуры, ограниченной заданными линиями:

$\displaystyle y=\frac{1}{8}x^3;\;\;\;y=3-x;\;\;\;y=-4x.$

равна 5 ед.²

Объяснение:

Вычислите площадь фигуры, ограниченной заданными линиями:

$\displaystyle y=\frac{1}{8}x^3;\;\;\;y=3-x;\;\;\;y=-4x.$

Определим искомую фигуру.

Построим графики.

$\displaystyle 1.\;\;\;y=\frac{1}{8}x^3$

- кубическая функция, график - кубическая парабола.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| c|}\cline{1-4}x& 0 & 2 & 3 \\\cline{1-4}y& 0& 1 & \frac{27}{8} \\\cline{1-4}\end{array}$

Вторая ветвь симметрична относительно начала координат.

$\displaystyle 2.\;\;\;y=3-x$

- линейная функция, график - прямая.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| }\cline{1-3}x& 1 & 3 \\\cline{1-3}y& 2 & 0 \\\cline{1-3}\end{array}$

$3.\;\;\;y=-4x$

- линейная функция, график - прямая.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| }\cline{1-3}x& 1 & -1 \\\cline{1-3}y& -4 & 4 \\\cline{1-3}\end{array}$

Получили фигуру, состоящую из двух частей, одна из которых ограничена снизу графиком у = -4х, другая у =(1/8)х³

4. Найдем абсциссу точки пересечения первого и второго графика:

$\displaystyle \frac{1}{8}x^3=3-x\;\;\;|\cdot8\\ \\x^3=24-8x\\\\x^3+8x-8-16=0\\\\(x-2)(x^2+2x+4)+8(x-2)=0\\\\(x-2)(x^2+2x+12)=0\\\\x^2+2x+12 > 0\\\\x-2=0\\\\x=2$

Найдем абсциссу точки пересечения первого и третьего графика:

$\displaystyle \frac{1}{8}x^3=-4x\;\;\;|\cdot8\\ \\x^3+32x=0\\\\x(x^2+32)=0\\\\x^2+32 > 0\\\\x=0$

Найдем абсциссу точки пересечения второго и третьего графика:

3 - х = -4х

3(1 + х) = 0

х = -1

5. Найдем площадь фигуры по формуле:

$\displaystyle \boxed { S=\int\limits^b_a {(f_2(x)-f_1(x))} \, dx }$

$\displaystyle S=S_1+S_2=\int\limits^{0}_{-1} {(3-x+4x)} \, dx +\int\limits^2_0 {(3-x-\frac{1}{8}x^3) } \, dx =\\\\=(3x+3\cdot\frac{x^2}{2})\bigg|^0_{-1} +(3x-\frac{x^2}{2}-\frac{1}{8}\cdot\frac{x^4}{4})\bigg|^2_0\\ \\ = (3x+\frac{3x^2}{2})\bigg|^0_{-1} +(3x-\frac{x^2}{2}-\frac{x^4}{32})\bigg|^2_0\\\\0-(-3+\frac{3}{2})+6-2-\frac{1}{2} -0=5$