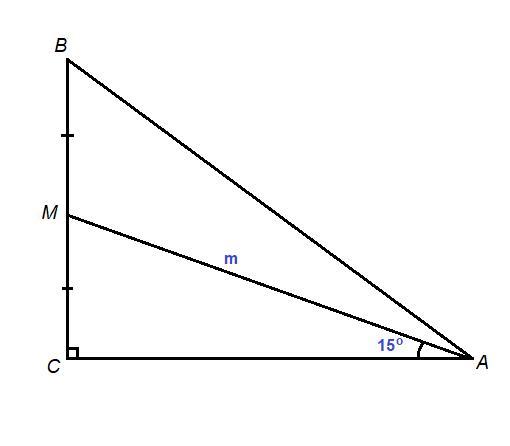
< >

У прямокутному трикутнику АВС ∠C=90° медіана АМ, проведена до меншого катета, утворює з більшим катетом кут 15°. Знайдіть площу трикутника ABC, якщо АМ = m.

Ответы

Ответ дал: KuOV

Ответ:

$\boldsymbol{S_{ABC}=\dfrac{m^2}{4}}$

Объяснение:

Из прямоугольного треугольника АМС:

$\cos\angle MAC = \dfrac{AC}{AM}$

$AC=AM\cdot \cos\angle AMC$

$AC=m\cdot \cos 15^\circ$

Площадь треугольника равна половине произведения его сторон на синус угла между ними.

$S_{AMC}=\dfrac{1}{2}AM\cdot AC\cdot \sin\angle AMC$

$S_{AMC}=\dfrac{1}{2}m\cdot m\cdot \cos 15^\circ\cdot \sin 15^\circ$

По формуле синуса двойного угла:

$\sin 2\alpha=2\sin\alpha\cos\alpha$

Тогда

$\sin\alpha\cdot \cos\alpha =\dfrac{1}{2}\sin 2\alpha$

$\sin 15^\circ\cdot \cos15^\circ =\dfrac{1}{2}\sin 30^\circ$

$S_{AMC}=\dfrac{1}{2}\cdot m^2\cdot \dfrac{1}{2}\sin 30^\circ=\dfrac{1}{2}\cdot m^2\cdot \dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{m^2}{8}$

$\boldsymbol{S_{ABC}}=2S_{AMC}=2\cdot \dfrac{m^2}{8}\boldsymbol{=\dfrac{m^2}{4}}$

Приложения:

Похожие вопросы

Математика

1 год назад

Химия

1 год назад

Английский язык

2 года назад

Другие предметы

2 года назад

Математика

7 лет назад

География

7 лет назад

История

8 лет назад

География

8 лет назад