Используя известные разложения записать ряд Тейлора для функции в точке хо Указать радиус и интервал сходимости полученного ряда.

Приложения:

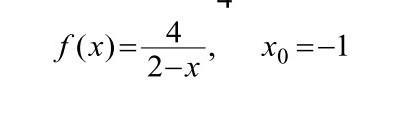
Ответы

Ответ дал: NNNLLL54

Ответ:

$f(x)=\dfrac{4}{2-x}\ \ ,\ \ x_0=-1$

Так как $x_0=-1$ , то разложить функцию в ряд Тейлора надо по

степеням $(x-x_0)=(x+1)$ .

Чтобы воспользоваться уже известными разложениями функций в ряд Маклорена, сделаем замену $\tilde{x}=x+1\ \ \ \to \ \ \ x=\tilde{x}-1$ .

Тогда $f(x)=\dfrac{4}{2-x}=\dfrac{4}{2-(\tilde{x}-1)}=\dfrac{4}{3-\tilde{x}}=\dfrac{4}{3\cdot (1-\dfrac{\tilde{x}}{3})}=\dfrac{4}{3}\cdot \dfrac{1}{1-\dfrac{\tilde{x}}{3}}$ .

Воспользуемся известным разложением в ряд Маклорена

$\dfrac{1}{1-t}=1+t+t^2+t^3+...+t^{n}+...\ \ ,\ \ -1 < t < 1\ -\ interval\ sxodimosti$ ,

причём $t=\dfrac{\tilde{x}}{3}$ .

$\displaystyle f(x)=\frac{4}{3}\cdot \Big(1+\frac{\tilde{x}}{3}+\Big(\frac{\tilde{x}}{3}\Big)^2+\Big(\frac{\tilde{x}}{3}\Big)^3+\Big(\frac{\tilde{x}}{3}\Big)^4+...+\Big(\frac{\tilde{x}}{3}\Big)^{n}+...\Big)=\\\\\\=\frac{4}{3}\cdot \Big(1+\frac{\tilde{x}}{3}+\frac{\tilde{x}^2}{3^2}+\frac{\tilde{x}^3}{3^3}+\frac{\tilde{x}^4}{3^4}+...+\frac{\tilde{x}^{n}}{3^{n}}+...\Big)=$

$\displaystyle =\frac{4}{3}+\frac{4\tilde{x}}{3^2}+\frac{4\tilde{x}^2}{3^3}+\frac{4\tilde{x}^3}{3^4}+\frac{4\tilde{x}^4}{3^5}+...+\frac{4\tilde{x}^{n}}{3^{n+1}}+...$

Сделаем обратную замену $\displaystyle \tilde{x}=x+1$ , получим ряд

$f(x)\sim \dfrac{4}{3}+\sum \limits _{n=1}^{\infty }\, \dfrac{4(x+1)^{n}}{3^{n+1}}$ .

Интервал сходимости ряда: $-1 < \dfrac{\tilde{x}}{3} < 1\ \ \Rightarrow \ \ \ -3 < \tilde{x} < 3\ \ ,\ \ -3 < x+1 < 3\ \ ,\ \ \underline{-4 < x < 2}$

При х=2: $\dfrac{4}{3}+\sum \limits _{n=1}^{\infty }\, \dfrac{4\cdot 3^{n}}{3^{n+1}}=\dfrac{4}{3}+\sum \limits _{n=1}^{\infty }\, \dfrac{4}{3}$ - расходящийся ряд, не выполняется необходимый признак сходимости .

При х= -4: $\dfrac{4}{3}+\sum \limits _{n=1}^{\infty }\, \dfrac{4\cdot (-3)^{n}}{3^{n+1}}=\dfrac{4}{3}+\sum \limits _{n=1}^{\infty }\, \dfrac{(-1)^{n}\cdot 4}{3}$ - расходящийся ряд, не выполняются условия признака Лейбница .