помогите решить неравенства
Приложения:
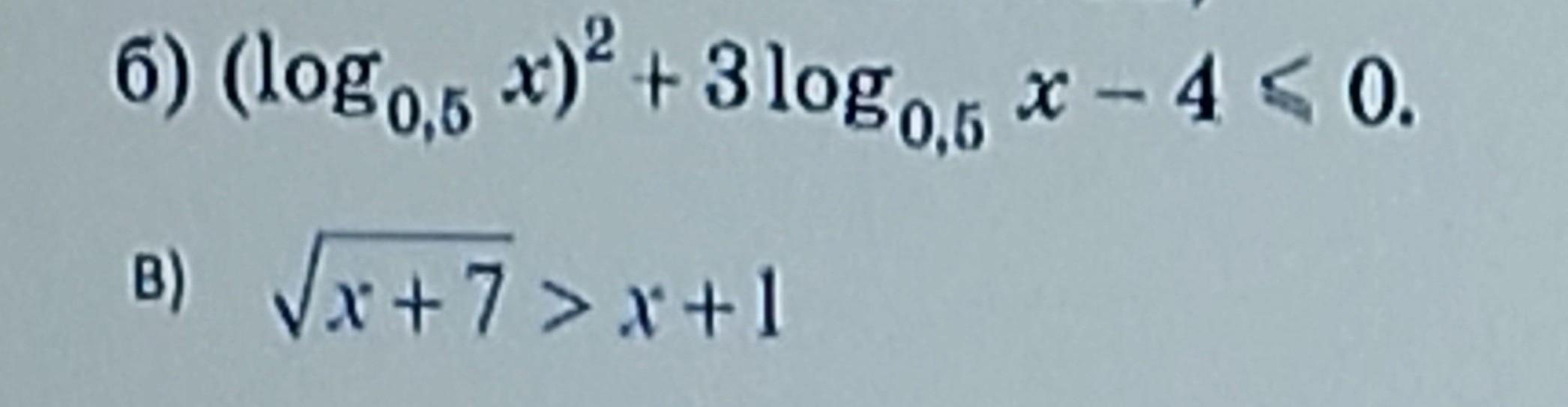
Аноним:
На коли? Терміново?
желательно было бы как можно скорее
Ответы
Ответ дал:
1
Ответ:
Б) х ∈ [0,5, 16].
В) х ∈ [-7, 2⟩.
Неравенство Б:
(log₀,₅х)² + 3log₀,₅x - 4 ≤ 0
Область допустимых значений — х > 0.
Заменяем log₀,₅x на t и упрощаем —
Далее ,
.
Находим пересечение — ∅, t ∈ [-4, 1].
Подставляем обратно — log₀,₅x ∈ [-4, 1].
Записываем интервал в виде неравенства —
Решаем — ,
.
Находим пересечение — х ∈ [0,5, 16], х > 0.
Неравенство В:
Область допустимых значений — х ≥ -7.
Разделяем неравенство на 2 возможных случая —
.
Решаем неравенства —
х ∈ ⟨-3, 2⟩, х ≥ -1; х ∈ ℝ, х < -1.
Находим пересечение —
х ∈ [-1, 2⟩; х ∈ ⟨-∞, -1⟩.
Находим объединение —
х ∈ ⟨-∞, 2⟩, х ≥ -7.
Находим пересечение — х ∈ [-7, 2⟩.
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад