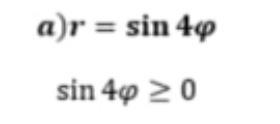Ответы
Ответ дал:
1
Ответ:
восьмилепестковая роза
Объяснение:
Этот график называется полярная роза. (Розы Гранди)
Семейство кривых, уравнение которых имеет вид
Здесь а - радиус розы, Если k — целое число, то это уравнение будет определять розу
- с k лепестками для нечётных k,
- либо с 2k лепестками для чётных k.
Таким образом мы получим 8-лепестковую розу радиусом 1
Посмотрим на период функции
Каждая точка характеризуется координаиами .
Точка пробегает по кругу от 0 до 2п против часовой стрелки.
Функция имеет максимумы в точках
.
Это "вершины" лепестков.
Учитывая период фкнуции Т = п/2, можно построить график для первой четверти и потом симметрично отобразить его на остальной круг.
Приложения:
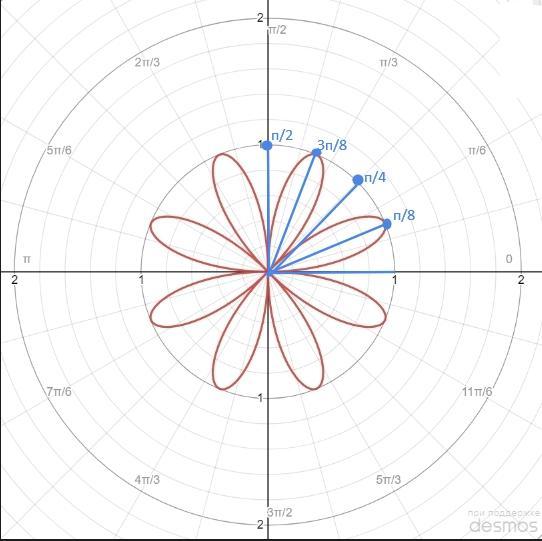
так как r >= 0 , то 4 лепестка будет
Да, 4 лепестка
Похожие вопросы
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
8 лет назад
8 лет назад