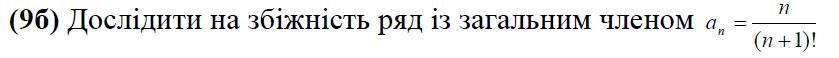Дослідити на збіжність ряд із загальним членом

Ответ:

ряд сходится

Пошаговое объяснение:

Признак Даламбера

Если существует предел отношения последующего члена к предыдущему:  , то:

• - при q < 1 ряд сходится (в частности, ряд сходится при q=0);
• - при  q > 1 ряд расходится (в частности, ряд расходится при
•   q = ∞);
• - при  q = 1 признак не дает ответа.

Найдем  

Сначала найдем отношение

И теперь предел этого отношения

Вывод: q < 1, значит   ряд сходится

#SPJ1