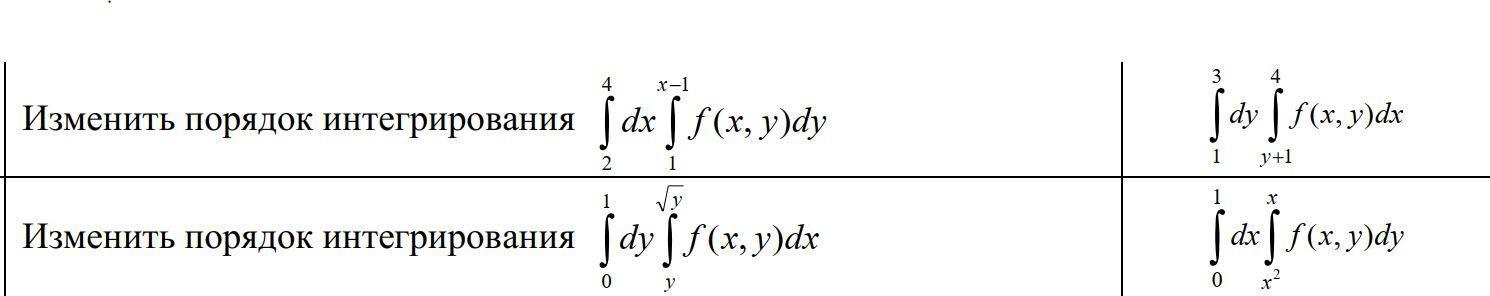Ответы
Ответ дал:
0
Ответ:
ответы в объяснениях
Объяснение:
1) Для изменения порядка интегрирования построим область интегрирования.
2 ≤ x ≤ 4; 1 ≤ y ≤x-1
у = х - 1 ⇒ х = у + 1
Теперь по графику мы видим, что у нас изменяются
у от 1 до 3
х от у+1 до 4
Тогда мы получим
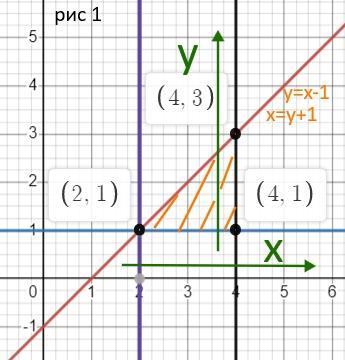
рис 1
2)
x=√y ⇒ y = x²
х = у
Область интегрирования
0 ≤ y ≤ 1; y ≤ x ≤ √y
Определяемся с новыми границами.
х изменяется от 0 до 1
у изменяется от х² до х
рис 2
3)
х = у + 1 ⇒ у = х - 1
Область интегрирования
1 ≤ y ≤ 3
y+1 ≤ x ≤ 4
По графикам определяем новые пределы интегрирования
2 ≤ x ≤ 4
1 ≤ y ≤ x - 1
Получаем
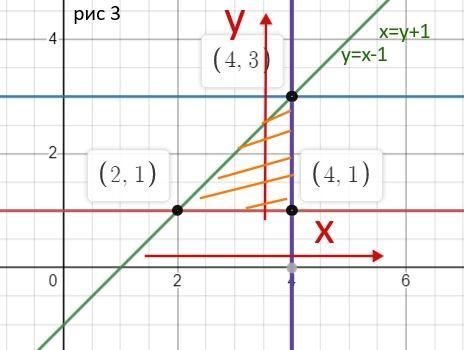
рис 3
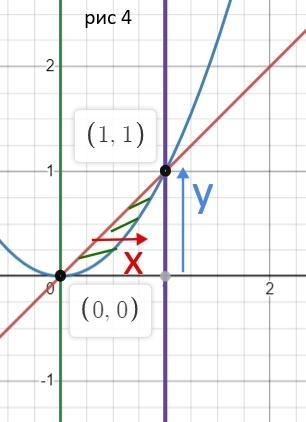
4)
y = x
y=x² x=√y
Область интегрирования
x² ≤ y ≤ x
0 ≤ x ≤ 1
По графикам определяем новые пределы интегрирования
√y ≤ x ≤ y
0 ≤ y ≤ x 1
Получаем
рис 4
#SPJ1
Приложения:
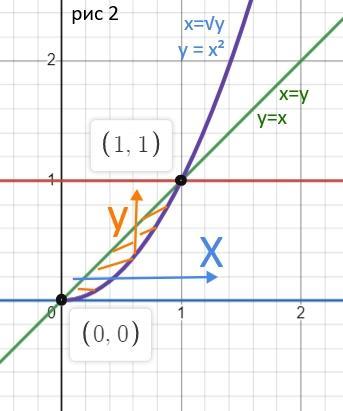
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
8 лет назад