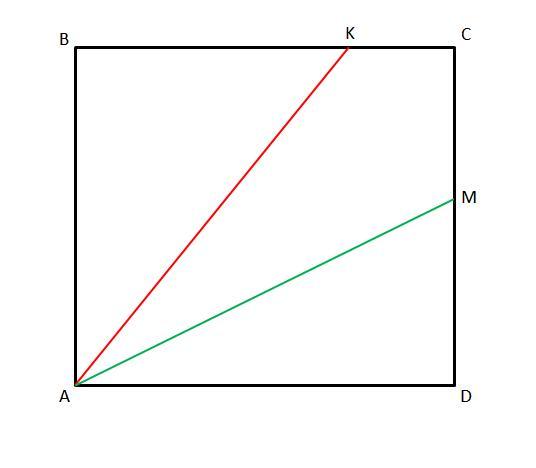
АВCD квадрат. Точка М лежит на стороне СD. Биссектриса угла ВАМ пересекает сторону ВС в точке К. Доказать что АМ = BK + DM

Ответ:

Пусть сторона квадрата _ а ( AB = BC = CD = AD = a)

поскольку АК биссектриса угла ВАМ ⇒ ∠ВАК = ∠КАМ

пусть ∠ВАК = х ⇒ ∠ВАК = ∠КАМ = х

Из прям. треугольника АВК

ВК = АВ · tan ·x

∠MAD = 90° - ( ∠ВАК + ∠КАМ ) = 90° - 2x

Из прям. треугольника AMD

MD = AD · tan∠MAD = a · ( 90° - 2x )

= =

AM =  

=>

AM = BK + DM =