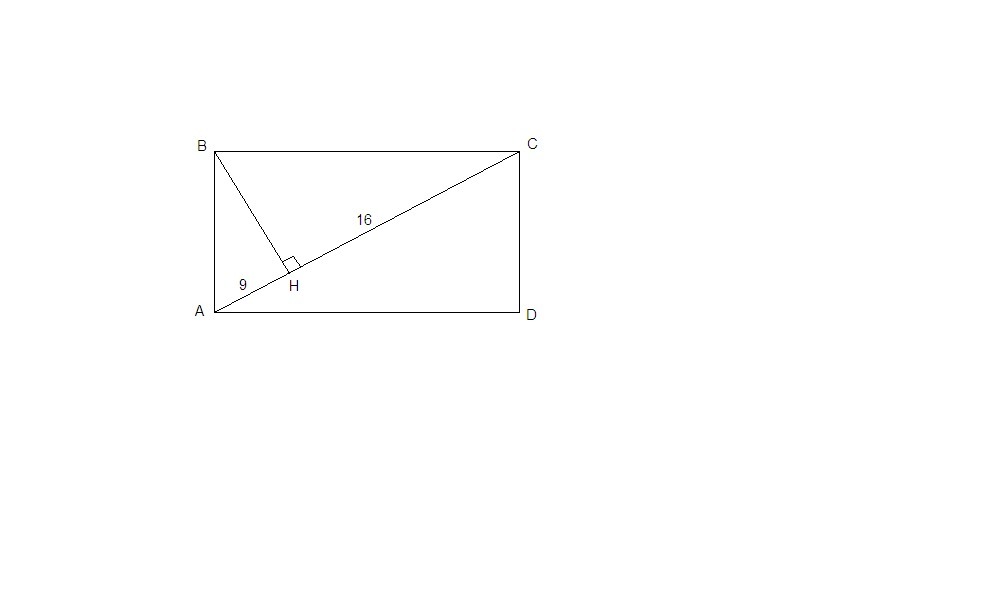
Из вершины прямоугольника на диагональ опущен перпендикуляр,который делит ее на отрезки длинной 9 см и 16 см. Найдите тангенс угла,образованного меньшей стороной и диагональю.

ΔАВС прямоугольный, ВН - высота прямоугольного треугольника.
Высота прямоугольного треугольника, опущенная на гипотенузу равна среднему геометрическому отрезков, на которые она разделила гипотенузу:
ВН² = АН · НС
ВН = √(9 · 16) = 3 · 4 = 12

Из прямоугольного треугольника АВН:
tg BAH = BH / AH = 12 / 9 = 4/3