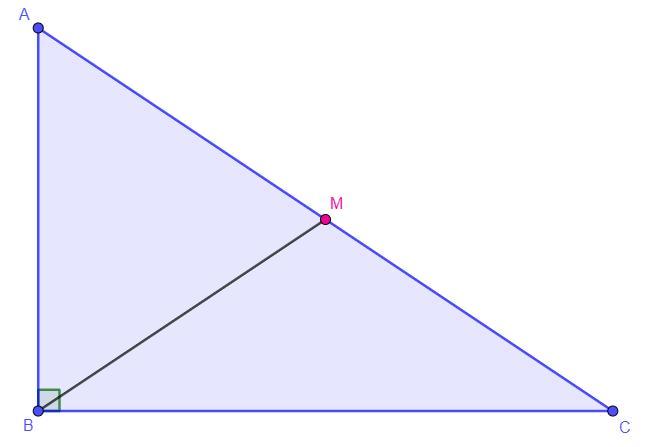
Медіана, проведена до гіпотенузи прямокутного трикутника ділить прямий кут у відношенні 1:2 і дорівнює 16 см. обчислять сторони трикутника.

Ответы

Ответ дал: mathkot

Відповідь:

Сторони трикутника дорівнють 32 см, 16 см і $\boldsymbol{16\sqrt{3}}$ см

Пояснення:

Дано: ∠ABC = 90°, ∠CBM : ∠ABM = 1 : 2, BM = 16 см, BM - медіана

Знайти: AB, BC, AC - ?

Розв'язання:

Так як за умовою кут ∠ABC = 90°, то за означенням трикутник

ΔABC - прямокутний.

Так як за умовою кут ∠CBM : ∠ABM = 1 : 2, то введемо коефіцієнт пропрційності х, тоді кут ∠CBM = х і кут ∠ABM = 2x.

∠CBM + ∠ABM =∠ABC

x + 2x = 90°

3x = 90°|:3

x = 30°

Отже, ∠CBM = х = 30°, ∠ABM = 2x = 2 · 30° = 60°.

За означенням медіани, так як за умовою BM - медіана, то AM = MC.

За властивостями прямокутного трикутника (трикутник ΔABC - прямокутний) медіана проведена до гіпотенузи дорівнює половині гіпотенузи, звідси AC = 2BM = 2 · 16 см = 32 см і AM = MC = BM = 16 см.

За означенням трикутник ΔBMC - рівнобедрений, так як BM = MC, тоді за властивостями рівнобедреного трикутника кути про основі рівні, отже кут ∠MBC = ∠ACB = 30°.

Розглянемо прямокутний трикутник ΔABC.

За означенням косинуса у прямокутному трикутнику:

$\cos \angle ACB = \dfrac{BC}{AC} \Longrightarrow BC = AC\cos \angle ACB = 32 \cdot \cos 30^{\circ} = \dfrac{32\sqrt{3} }{2} = 16\sqrt{3}$ см.