Предмет: Алгебра
Автор: kimkarina953
Вопрос задан 2 года назад

< >

помогите пожалуйста с номером 53

Приложения:

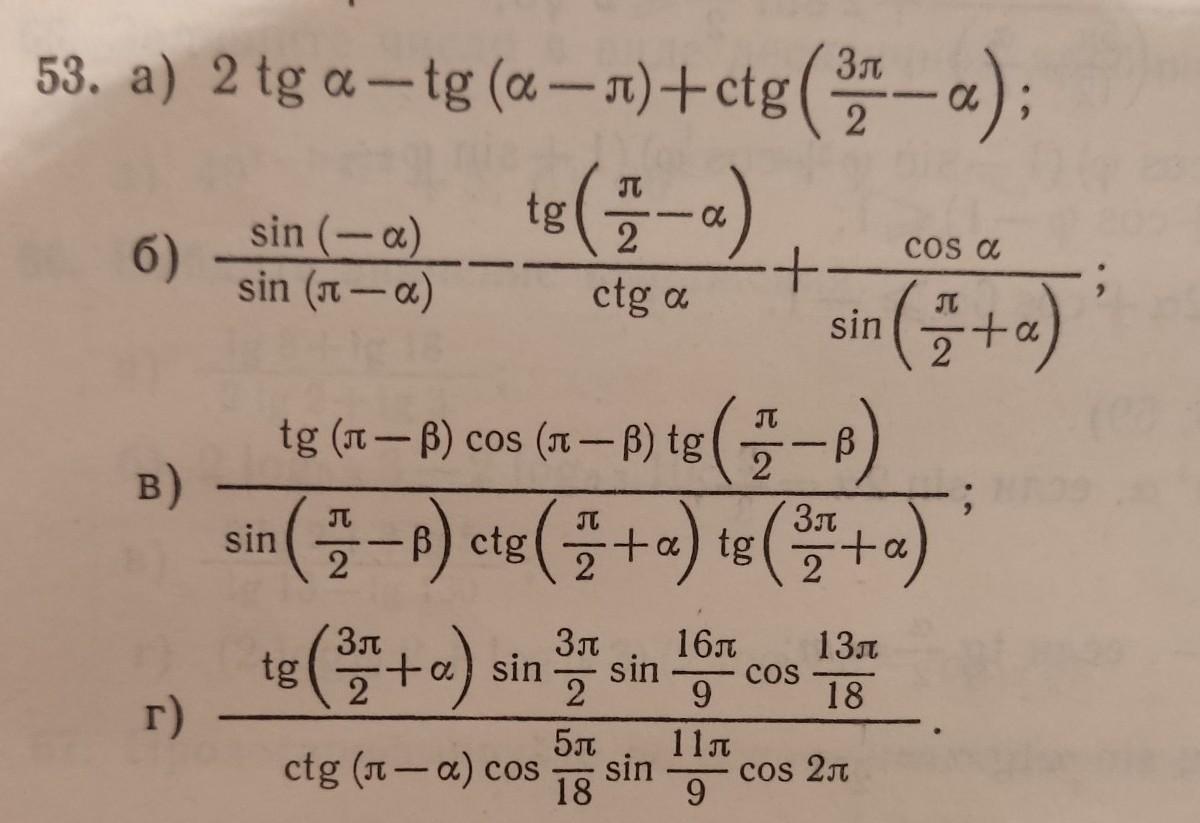
kukuiashnamariana: що за урок такой

kimkarina953: алгебра

kukuiashnamariana: автор книги и какой клас

Ответы

Ответ дал: Universalka

1

$\displaystyle\bf\\1)\\\\2tg\alpha -tg\Big(\alpha -\pi \Big)+Ctg\Big(\frac{3\pi }{2} -\alpha \Big)=2tg\alpha -tg\alpha +tg\alpha =2tg\alpha \\\\2)\\\\\frac{Sin(-\alpha )}{Sin(\pi -\alpha )} -\frac{tg\Big(\frac{\pi }{2} -\alpha \Big)}{Ctg\alpha }+\frac{Cos\alpha }{Sin\Big(\frac{\pi }{2} +\alpha \Big)} =\frac{-Sin\alpha }{Sin\alpha } -\frac{Ctg\alpha }{Ctg\alpha } +\frac{Cos\alpha }{Cos\alpha } =\\\\\\=-1-1+1=-1$

$\displaystyle\bf\\3)\\\\\frac{tg(\pi -\beta ) Cos(\pi -\beta ) tg\Big(\frac{\pi }{2} -\beta \Big)}{Sin\Big(\frac{\pi }{2}-\beta \Big) Ctg\Big(\frac{\pi }{2} +\alpha \Big) tg\Big(\frac{3\pi }{2} +\alpha\Big) } =\frac{-tg\beta\cdot (-Cos\beta )\cdot Ctg\beta }{Cos\beta \cdot (-tg\alpha )\cdot (-Ctg\alpha )} =\\\\\\=\frac{Cos\beta }{Cos\beta } =1\\\\\\4)$

$\displaystyle\bf\\\frac{tg\Big(\frac{3\pi }{2} +\alpha \Big) Sin\frac{3\pi }{2} Sin\frac{16\pi }{9} Cos\frac{13\pi }{18} }{Ctg(\pi -\alpha ) Cos\frac{5\pi }{18} Sin\frac{11\pi }{9}Cos2\pi } =\\\\\\=\frac{-Ctg\alpha \cdot (-1)\cdot Sin(2\pi -\frac{2\pi }{9} )\cdot Cos(\pi -\frac{5\pi }{18} ) }{-tg\alpha\cdot Cos\frac{5\pi }{18} \cdot Sin(\pi +\frac{2\pi }{9} )\cdot 1 } =$

$\displaystyle\bf\\=\frac{Ctg\alpha \cdot (-Sin\frac{2\pi }{9} )\cdot Cos\frac{5\pi }{18} }{-tg\alpha \cdot Cos\frac{5\pi }{18} \cdot(-Sin\frac{2\pi }{9} )} =-\frac{Ctg\alpha }{tg\alpha } =-\frac{Ctg\alpha }{\frac{1}{Ctg\alpha } } =-Ctg^{2}\alpha$

kimkarina953: Большое спасибо за оказанную помощь. Пусть ваша доброта будет оценена по заслугам.

Universalka: :))

kimkarina953: прошу прощения, что тревожу вас. Не могли бы помочь с задачей

Аноним: помогите пожалуйста с алгеброй очень надо дам лучший ответ

Похожие вопросы

Математика

1 год назад

1. Сумма длин всех ребер прямоугольного параллелепипеда равна 252 см, два его измерения -3 см и 7 см. Найдите третье измерение параллелепипеда.

Английский язык

1 год назад

составьте предложения на английском со словами chat with friends go online make video play games listen music

Русский язык

2 года назад

Слова с приставкой вес

Русский язык

2 года назад

КАК правельно записать: Я пришёл со школы и пошёл со своей гулять в наморднике.

Математика

7 лет назад

4(х - 7) - 2(1,5х + 4) = -30 x=?

Физика

7 лет назад

Физика. Сделать задание, с дано и решением. Двигатель самолета развивает мощность 4,4 * 10 ^ 4 кВт, при скорости 900 км / ч, и потребляет 2,04 тонны керосина на 100 км пути. Определите КПД

Математика

8 лет назад

скорость лодки по течению реки 9 км в час скорость течения реки 3 км в час сколько времени понадобится что бы на этой лодке проплыть 27 км по реке и вернутся обратно помогите

Физика

8 лет назад

Просто сделайте РИСУНОК к задаче, пожалуйста Два тела, массы которых одинаковы и равны 100g, связанные нитью, лежат на столе. На одно из них действует сила 5H. Определите силу упругости соединяющей