допоможіть будь ласка​

Ответ:

Доведено, що ОА=ОС

Объяснение:

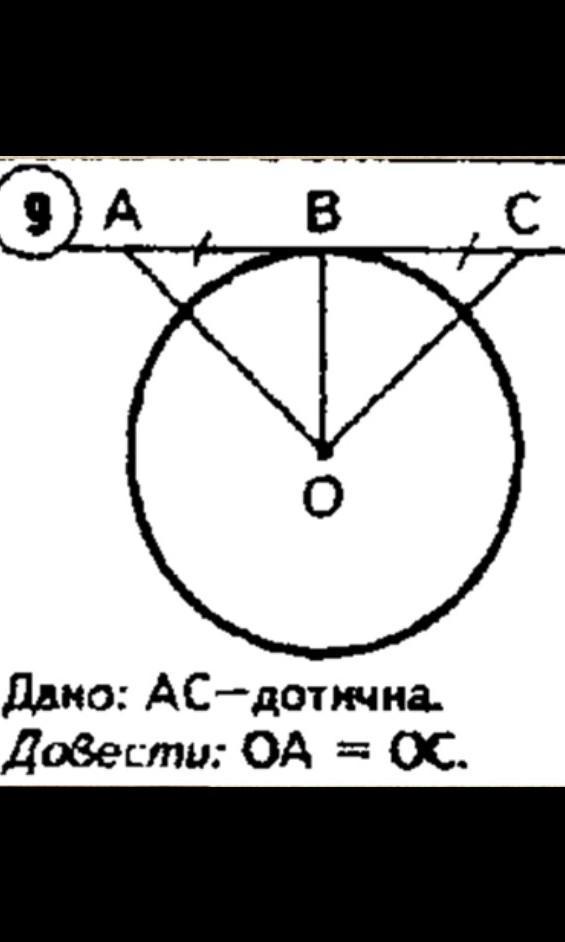
Дано: коло с центром в точці О, ОВ - ії радіус. AB=BC. АС - дотична

Довести: ОА=ОС

• Дотична до кола перпендикулярна до радіуса, проведеного в точку дотику.

За властивостю дотичної: АС⟂ОВ, тоді △АBO і △ CBO - прямокутні.

AB=BC - за умовою, OB - спільна, △ ABO=△CBO - за двома катетами.

Якщо трикутники рівні, то їх відповідні сторони рівні: OA=OC, що і треба довести.