помогите 100 баллов алвжвдвдвжв

Ответ:

АН = 3,5 ед

Объяснение:

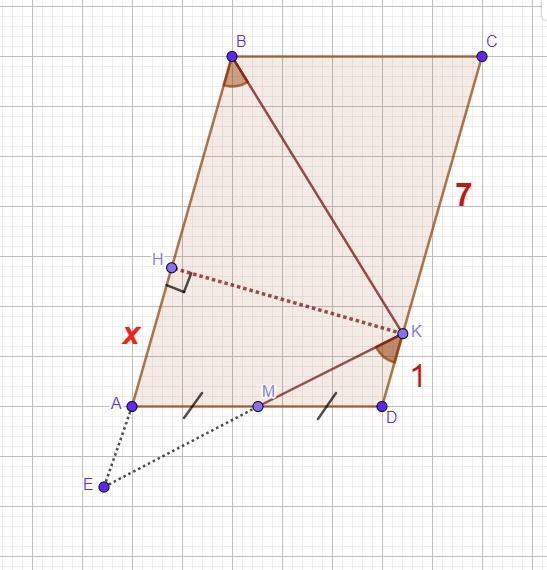
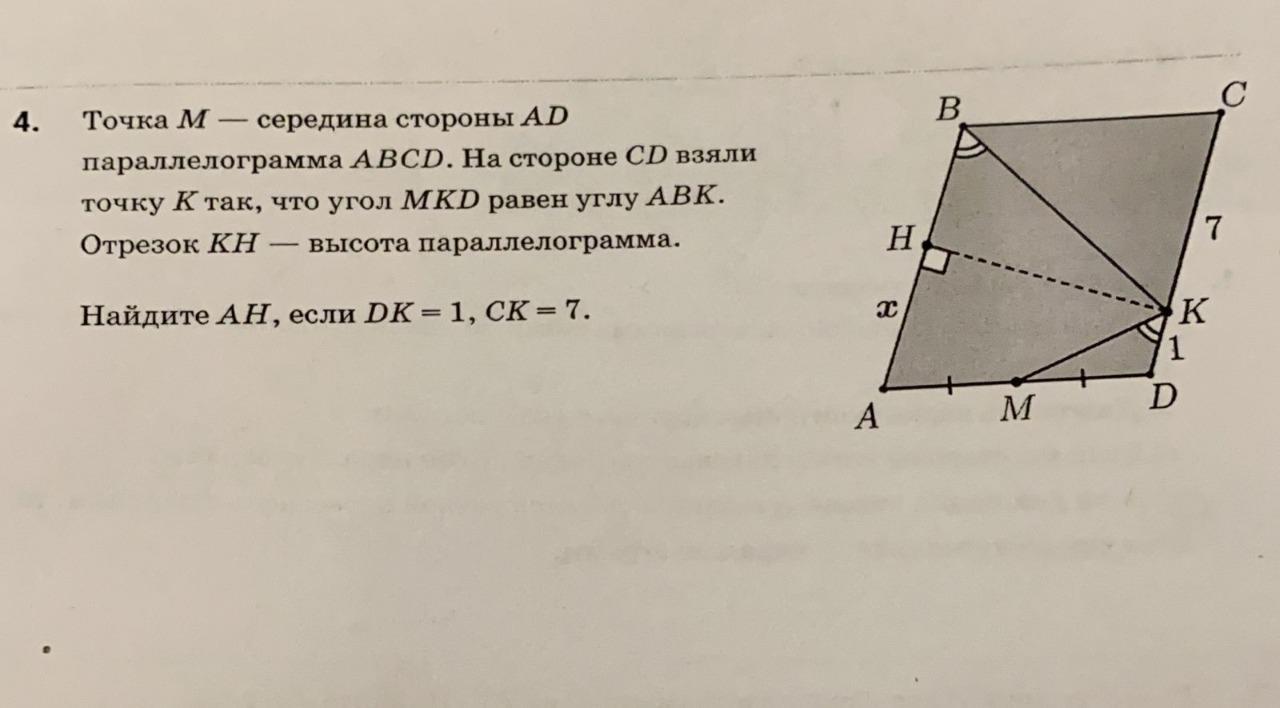
Точка М - середина стороны AD параллелограмма ABCD. На стороне СD взяли точку К так, что угол MKD равен углу АВК. Отрезок КН - высота параллелограмма.

Найдите АН, если DK=1, CК=7

• Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны.

Пусть прямые ВА и КМ пересекаются в точке Е.

Рассмотрим ΔMKD и ΔMEA.

• АМ=MD, по условию
• ∠АМЕ=∠КМD - как вертикальные
• ∠MKD =∠МЕА - как накрест лежащие углы, образованные при пересечении двух параллельных прямых прямых СD  и ВЕ секущей КЕ

ΔMKD = ΔMEA по стороне и двум прилежащим к ней углам (2 признак).

Из равенства треугольников следует равенство соответствующих элементов: АЕ=DK= 1.

ВЕ=ВА+АЕ, ВА=CD=СК+КD=7+1=8 - как противоположные стороны параллелограмма.

Значит ВЕ=8+1=9

Так как ∠MKD=∠МЕА (накрест лежащие углы), а ∠MKD=∠АВК - по условию, то ∠МЕА=∠АВК ⇒ ΔВКЕ - равнобедренный (по признаку), с основанием ВЕ.

НК - высота равнобедренного ΔВКЕ ⇒ она является также и медианой.

Таким образом, ВН=НЕ=ВЕ:2=9:2=4,5

Теперь находим х:

х =АН=ВА-ВН=8-4,5= 3,5 ед