прошу помогите даю 100 баллов задание легкое

Ответ:

АН равна 3,5 ед.

Объяснение:

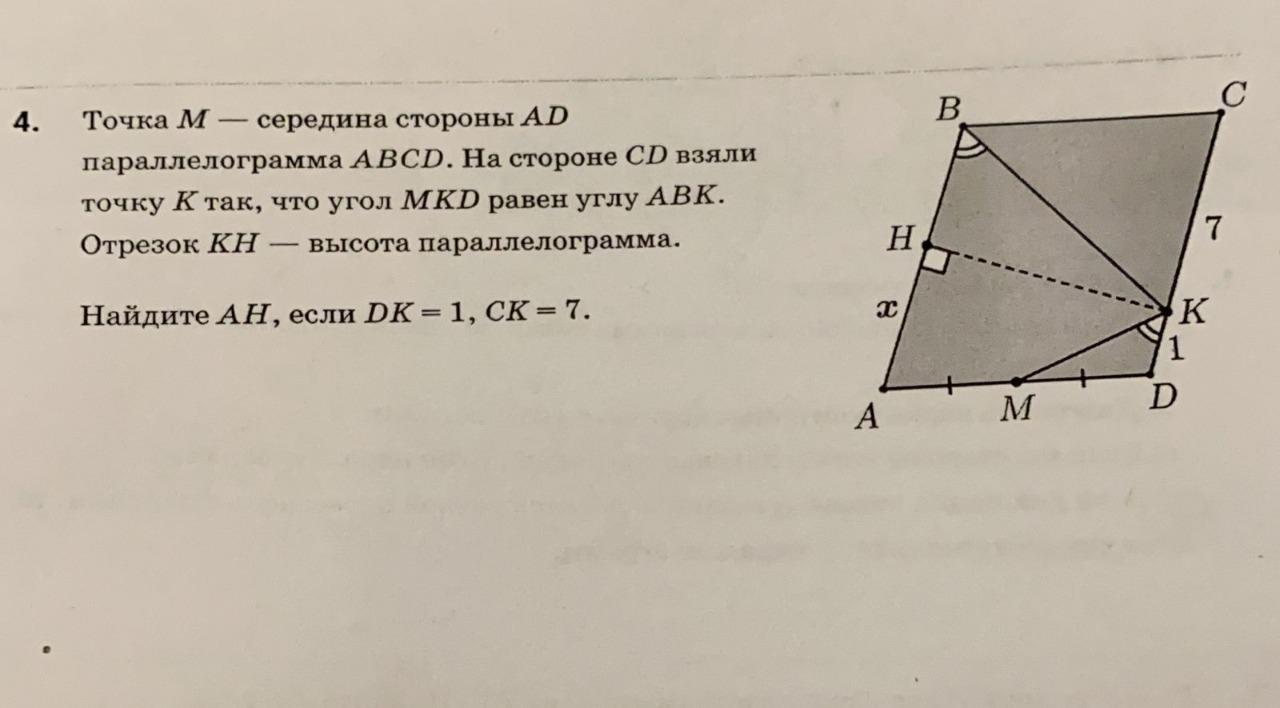
Требуется найти АН.

Дано: ABCD - параллелограмм;

АМ = МD;

K ∈ CD; ∠ABK = ∠MKD

KH - высота;

DK = 1; CK = 7.

Найти: АН.

Решение:

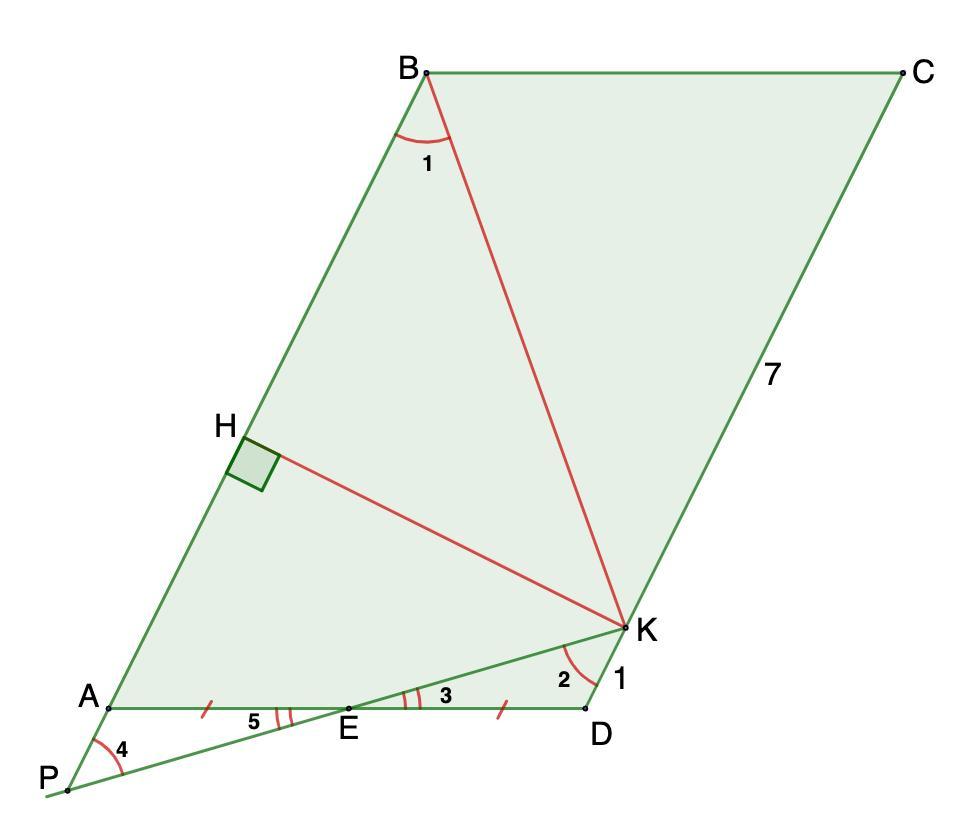
АВ ∩ КМ = Р

Для удобства обозначим углы цифрами (см. рис)

1. Рассмотрим ΔРАЕ и ΔЕКD.

AM = MD (условие)

• Вертикальные углы равны.

⇒ ∠5 = ∠3

• При пересечении двух параллельных прямых секущей накрест лежащие углы равны.

⇒ ∠РАМ = ∠МDK (накрест лежащие при РВ || DC и секущей AD)

ΔРАЕ = ΔЕКD (по стороне и двум прилежащим углам, 2 признак)

⇒ РА = DK = 1, ∠4 = ∠2 (как соответственные элементы)

2. Рассмотрим ΔРВК.

∠2 = ∠1 (условие)

∠2 = ∠4 (п.1)

⇒ ∠1 = ∠4

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ ΔРВК - равнобедренный.

• Противоположные стороны параллелограмма равны.

⇒ АВ = DC = 1 + 7 = 8

PB = РА +АВ = 1 + 8 = 9

КН - высота

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ РН = НВ = 9 : 2 = 4,5

АН = РН - РА = 4,5 - 1 = 3,5

АН равна 3,5 ед.