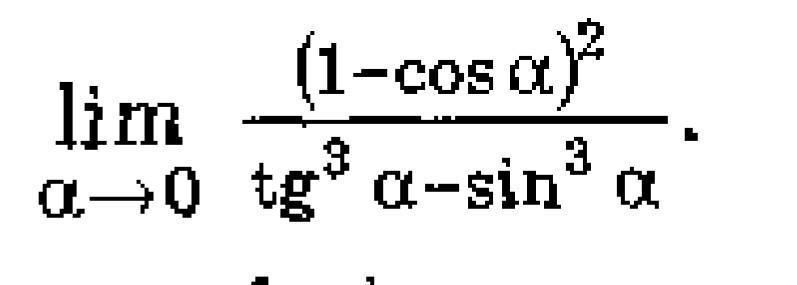Помогите найти предел

Ответ:

(см. объяснение)

Пошаговое объяснение:

Теперь вспоминаем про цепочку эквивалентностей и меняем:

• на
• на

Соответственно после сокращения получим:

(в последнем переходе мы вновь воспользовались цепочкой эквивалентности после того, как применили формулу разности кубов)

Итого пришли к лаконичному виду:

Найдем пределы с обеих сторон:

Поскольку левосторонний и правосторонний пределы различны, то заключаем, что исходного предела не существует.

Задание выполнено!