Предмет: Математика
Автор: kolaesaev
Вопрос задан 2 года назад

< >

Найдите какой-нибудь трёхзначный делитель числа 2^999+1.

Ответы

Ответ дал: genius20

1

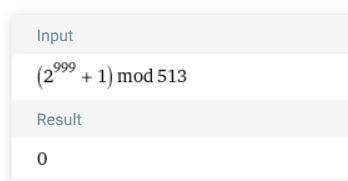
Рассмотрим сравнение по модулю 513:

$2^{999}+1 =(2^9)^{111}+1=512^{111}+1 \equiv (-1)^{111}+1=-1+1=0 \qquad (\text{mod }513)\\2^{999}+1 \equiv 0 \qquad (\text{mod }513)$

Ответ: 513.

На скриншоте проверка на компьютере.

Если что-нибудь непонятно — спрашивай.

Приложения:

Похожие вопросы

Русский язык

1 год назад

неосложненное или не осложненное и почему

Русский язык

1 год назад

Какое окончание в словах: Свежему Хорошему Рыжему Старшем

Қазақ тiлi

2 года назад

нууу умоляяяяю помогите перевести срочно очень нужно

Английский язык

2 года назад

отмет какие их этих команд и просьб выполнены неаерно

Математика

7 лет назад

Сумма числа и -13 равна 29. найдите число.

Другие предметы

7 лет назад

На какие территориальные единицы делится наша страна как она называется? Назовите область Республика Казахстан.Узнаете что есть особенность в области в котором вы проживаете.

Информатика

8 лет назад

дано целое число n и массив случайных чисел x[1..n].все элементы,меньше 2,заменить нулями.Кроме того,получить сумму и количество элементов,п ринаднежащих отрезку [3;7]

История

8 лет назад

помогите ответить на вопросы: 1)Как индийцы объяснили возникновение каст? 2)Как вера в переселения душ вынуждала индийцев заботиться о своих поступках и поведении? 3)Какой народ придумал шахматы и