У рівносторонній трикутник вписано ромб, який має з ним спільний кут. а) Знайдіть периметр ромба, якщо периметр трикутника дорівнює 24 см; б) знайдіть довжини відрізків, на які вершини ромба ділять сторони трикутника.

Решение .

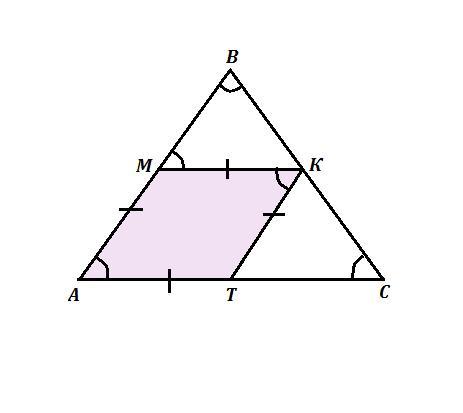
 ΔАВС - равносторонний  ⇒  АВ=ВС=АС , ∠А=∠В=∠С=60°  ,

Р(АВС)=24 см .

АМКТ - ромб  ⇒  АМ=МК=КТ=АТ ,  ∠МАТ=∠МКТ=60°  

Обозначим сторону ромба через  х=АМ=МК=КТ=АТ .

Тогда ВМ=8-х  см .

Так как противолежащие стороны ромба параллельны , то АТ || МК .

Тогда  ΔАВС ~ ΔМВК  по двум углам ( ∠В - общий , ∠ВАТ=∠ВМК как соответственные углы при АТ || МК и секущей АВ  ⇒  пропорциональность соответствующих сторон .

Сторона ромба равна 4, значит его периметр равен    см

б)  ВМ=АВ-АМ=8-4=4 см .

Так как АМ=МК=4 см , ∠ВМК=60° , то ΔМВК - равносторонний и

ВК=4 см . Тогда и КС=4 см , СТ=4 см .

Длины отрезков , на которые вершины ромба делят стороны треугольника равны 4 см .