Помогите пожалуйста срочно надо!!​

Ответ:

48 см²

Объяснение:

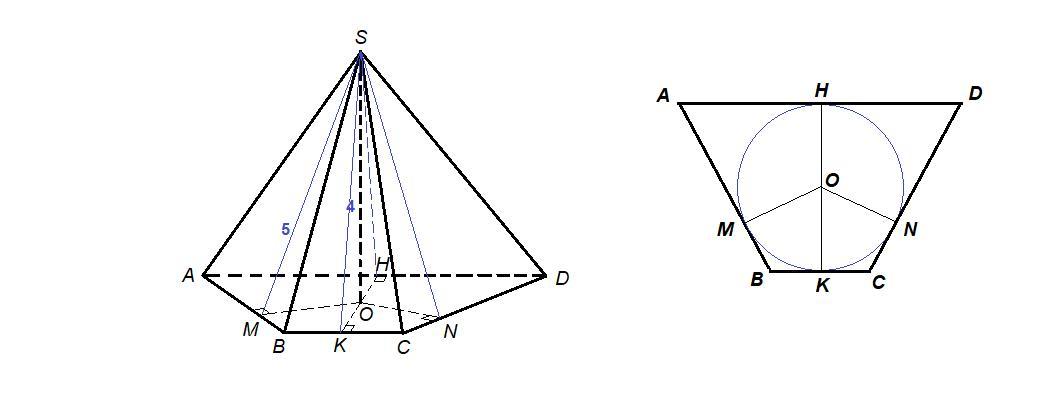
SO = 4 см - высота пирамиды.

Проведем SM, SK, SN и SH  высоты боковых граней.

По условию SM = SK = SN = SH = 5 см

Тогда и OM = OK = ON = OH как проекции равных наклонных, проведенных из одной точки, а так же эти отрезки перпендикулярны сторонам трапеции по теореме, обратной теореме о трех перпендикулярах.

Тогда точка О равноудалена от сторон трапеции, значит это центр окружности, вписанной в основание.

Можно просто запомнить:

• Если высоты боковых граней пирамиды равны, то высота пирамиды проецируется в центр окружности, вписанной в основание пирамиды.

Из прямоугольного треугольника SMO по теореме Пифагора:

OM = √(SM² - SO²) = √(5² - 4²) = 3 см - радиус вписанной окружности.

Высота трапеции равна двум радиусам вписанной окружности:

КН = 2 · 3 = 6 см

• Если в четырехугольник можно вписать окружность, то суммы противоположных сторон равны.

AD + BC = AB + CD = 16 см

Площадь трапеции:

S = 8 · 6 = 48 см²