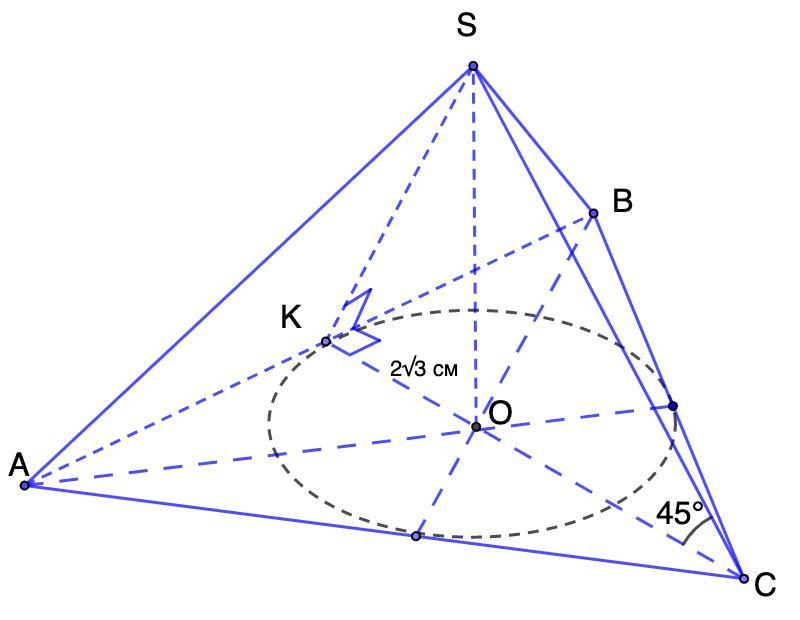
СРОЧНО!!!Радіус кола вписаного в основу правильної трикутної піраміди дорівнює 2√3 см бічне ребро утворює з площиною основи кут 45°. Знайдіть площу бічної поверхні піраміди​

Ответ:

====================

Ответ:

Площадь боковой поверхности равна 36√15 см².

Пошаговое объяснение:

Радиус окружности вписанного в основание правильной треугольной пирамиды равен 2√3 см. Боковое ребро образует с плоскостью основания угол 45°. Найдите площадь боковой поверхности пирамиды.

Дано: SABC - пирамида;

ΔАВС - правильный - основание пирамиды;

r = 2√3 см - радиус вписанной окружности;

∠SCO = 45°.

Найти: Sбок.

Решение:

, где Росн - периметр основания, d - апофема.

1. Рассмотрим ΔАВС - равносторонний.

Найдем сторону ΔАВС.

Радиус вписанной окружности равен:

, где а - сторона треугольника.

⇒ a = r · 2√3 = 2√3 · 2√3 = 12 (см)

Р(АВС) = 3а = 36 (см)

• В равностороннем треугольнике высоты являются медианами.

⇒ СК - медиана

• Высота треугольной пирамиды, проведенная из вершины, попадает на основание в центр пересечения медиан фигуры.

• Медианы точкой пересечения делятся в отношении 2 : 1, начиная от вершины.

⇒ ОС = 2 ОК = 2r = 4√3 (см)

2. Рассмотрим ΔOSC - прямоугольный.

∠SCO = 45°

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠CSO = 90° - 45° = 45°

• Если в треугольнике два угла равны, то этот треугольник - равнобедренный.

⇒ SO = OС = 4√3 см

3. Рассмотрим ΔКSO - прямоугольный.

По теореме Пифагора:

SК² = КО² + ОS² = 12 + 48 = 60

⇒ SK = √60 = 2√15 (см)

4. Знаем Р(АВС) = 36 см, d = SK = 2√15 см

Найдем площадь боковой поверхности:

 (см²)