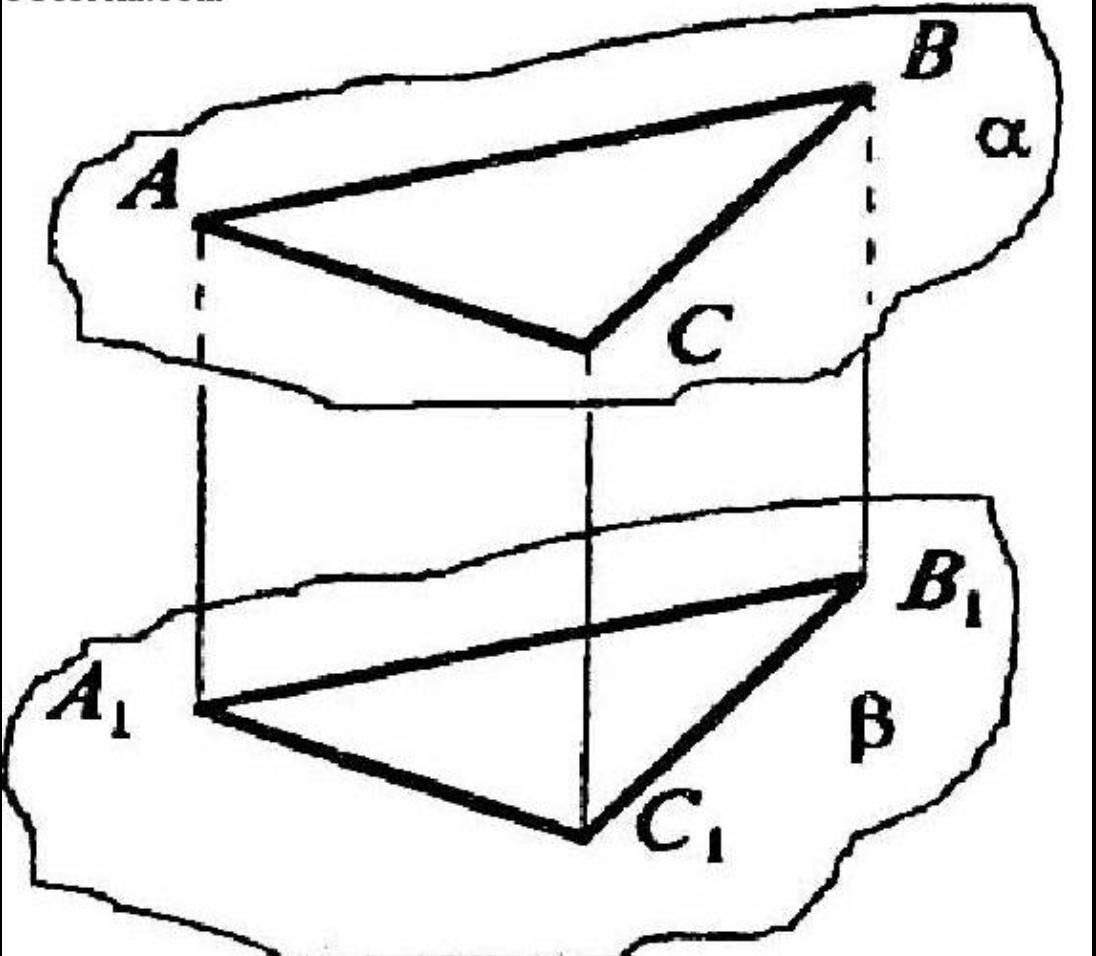
треугольник abc лежит в плоскости альфа через его вершины проведены параллельные прямые пересекаются плоскости бетта, параллельную плоскости альфа, в точке A1, B1 и C1. Доказать, что треугольники ABC и A1B1C1 равны.

Доказательство:

по свойству параллельных плоскостей, отрезки параллельных прямых заключенные между этими плоскостями равны, т.е. АА1=ВВ1=СС1 значит четырехугольники АА1В1В, ВВ1С1С и СС1А1А параллелограмы. Отсюда получаем что А1С1=АС, А1В1=АВ, В1С1=ВС. Таким образом треугольники АВС и А1В1С1 равны по трем сторонам. Что и требовалось доказать.