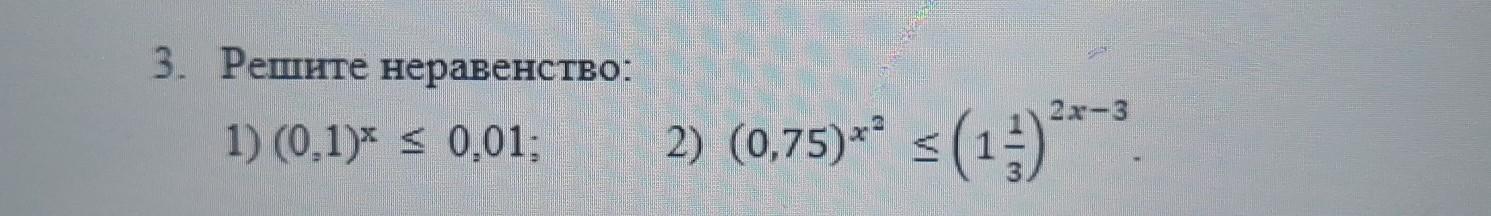СРОЧНО ПОМОГИТЕ ХЕЛП !!!

Приложения:

Ответы

Ответ дал: FaerVator

Ответ:

1) x∈[2;+∞)

2) x∈(-∞;-3]U[1;+∞)

Пошаговое объяснение:

$1)(0.1) ^{x} \leqslant 0.01$

Заметим , что 0,01 это 0,1²

$(0.1) ^{x} \leqslant 0.1 ^{2}$

Т.к основания степеней меньше 1 , значит , знак неравенства меняется на противоположный:

$(0.1) ^{x} \geqslant 0.1 ^{2} \\ x \geqslant 2 \\ x\in [2;+\infty )$

$2) \displaystyle (0.75) {}^{x ^{2} } \leqslant \Bigg( 1\frac{1}{3}\Bigg) ^{2x - 3}$

Представим левую часть в виде дроби , а правую часть превратим в неправильную дробь:

$\displaystyle \Bigg( \frac{3}{4} \Bigg) ^{x {}^{2} } \leqslant \Bigg( \frac{4}{3} \Bigg) ^{2x - 3}$

Чтобы в правой части превратить дробь в правильную - нужно еще поменять знаки показателя степени на противоположный :

$\displaystyle \Bigg( \frac{3}{4} \Bigg) ^{x {}^{2} } \leqslant \Bigg( \frac{3}{4} \Bigg) ^{ - 2x + 3}$

Основания степеней меньше 1 , тогда следует поменять знак неравенства :

$\displaystyle \Bigg( \frac{3}{4} \Bigg) ^{x {}^{2} } \geqslant \Bigg( \frac{3}{4} \Bigg) ^{ - 2x + 3} \\ x {}^{2} \geqslant - 2x + 3 \\ x {}^{2} + 2x - 3 \geqslant 0 \\ x {}^{2} + 2x - 3 = 0$

Данное квадратное уравнение без проблем можно решить через теорему Виета:

$\displaystyle \left. \begin{cases} { x_1 \cdot x_2 = - 3} \\ { x_1 + x_2 = - 2} \end{cases} \right. \Rightarrow x_1 = - 3 \: \: \: \: \: x_2 = 1 \\ x \in( - \infty; - 3]\text{U}[1;+\infty)$