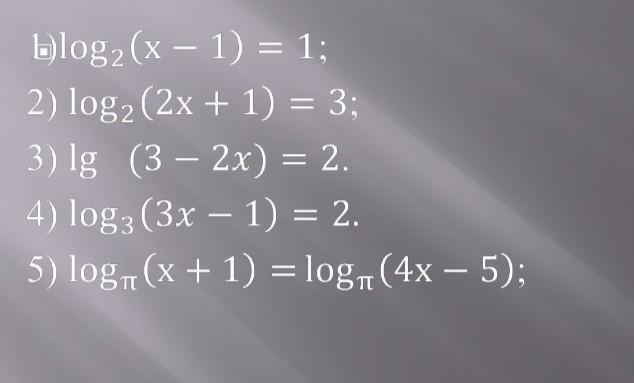Ответы
Ответ дал:
1
Ответ:
1)
2)
делим обе стороны уравнения на 2:
3)
делим обе стороны уравнения на -2:
4)
делим обе стороны уравнения на 3:
5)
делим обе стороны уравнения на -3:
himikomat:
Відзнач як найкращу відповідь будь ласка:)
дякую Вам. дуже вдячна
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад