Периметр треугольника АВС, описанного около окружности равен 36. Точка касания окружности со стороной ВС делит ее в отношении 2:5, считая от точки В, а точка касания со стороной АС удалена от точки А на 4. Найдите длину стороны АВ.
Ответы
Ответ дал:
0
см четреж.
ВМ = 2*х МС = 5*х, х - некая мера длины.
Тогда из свойств касательных
2*4 + 2*(2*х) + 2*(5*х) = 36; х = 2;
Отсюда АВ = 4 + 2*х = 8,
другие стороны обе по 14.
Приложения:
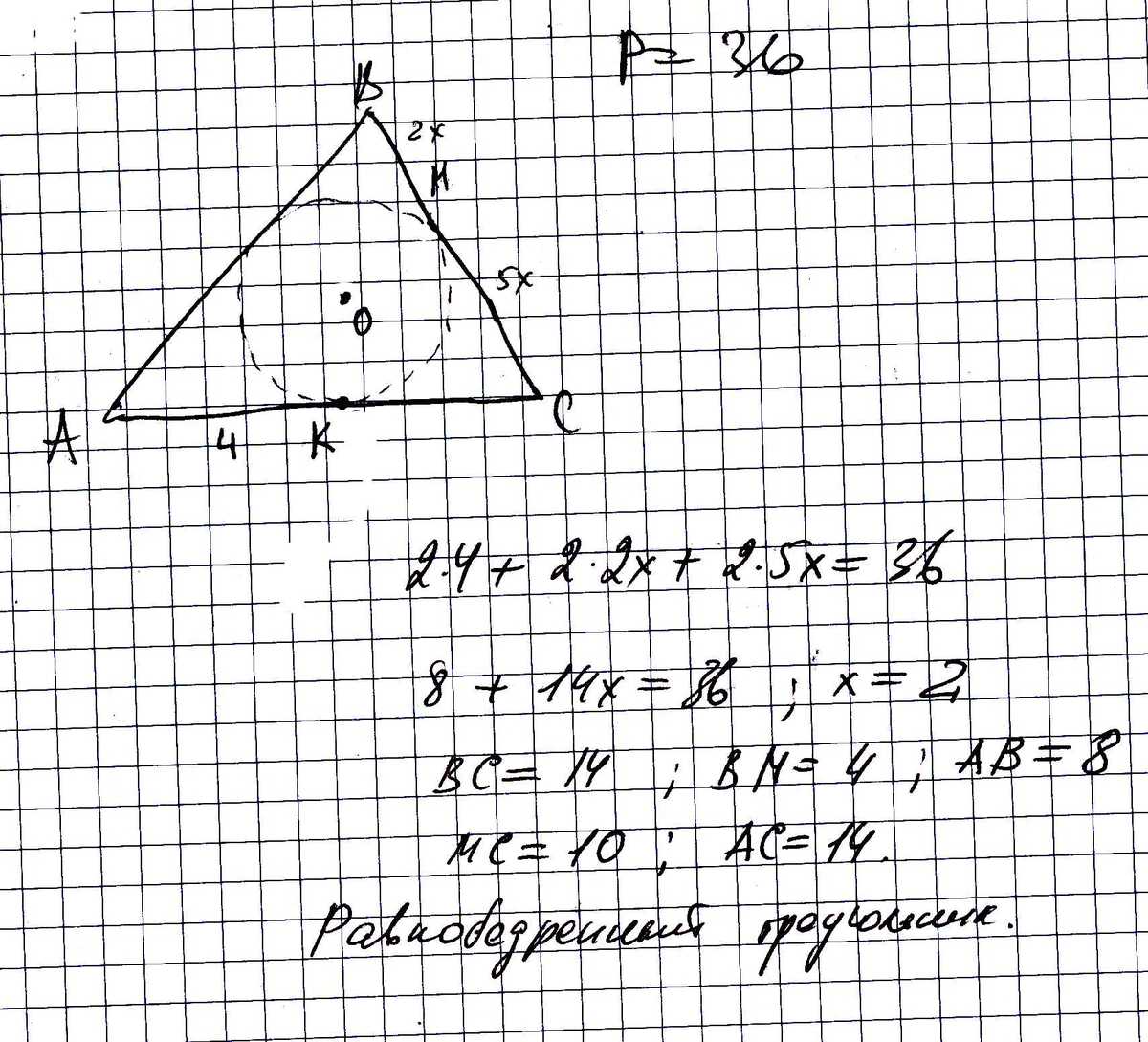
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад