7) У трапеції ABCD BC II AD, ABLAD, BC=CD, ZABD=80° Знайдіть кути трапеції. B С​

Объяснение:

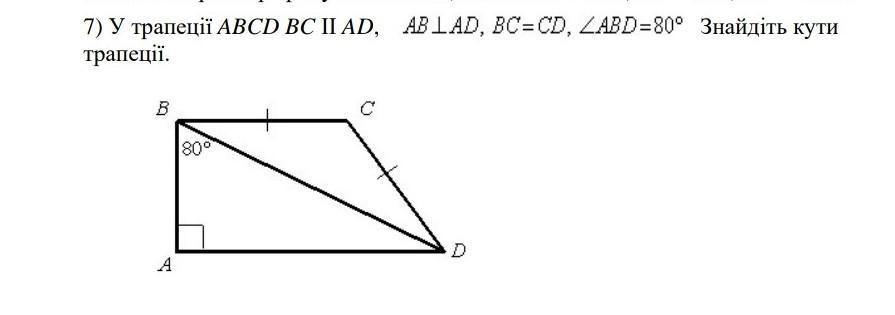
<A=90°, за умовою

<BDA=180°-<ABD-<A= 180°-80°-90°=180°-170°=10°, як сума кутів трикутника дорівнює 180°

<DBC=10°, як внутрішньо різносторонні

<B=<ABD+<DBC=80°+10°=90°

Отже трапеція ABCD - прямокутна. у прямокутної трапеції є 2 кути по 90°. Сума любого чотирикутника дорівнює 360°, отже

<C+<D=180°

трикутник BCD рівнобедрений, так як BC=CD(за умовою)

За властивістю рівнобедреного трикутника, кути при основі рівні, отже

<CDB=<CBD=10°, отже

<C=180°-20°=160°

<D=360°-<C-<B-<A=360°-160°-90°-90°=180°-160°=20°

Дано:

ABCD - трапеция

BC II AD

BC=CD

∠ABD=80°

Найти:

∠ B; ∠С​

----------------------------------------------------------------------------------------------------------

                                                 Решение:

∠A=90°

(по условию)

∠BDA = 180° - ∠ABD - ∠A = 180° - 80° - 90° = 180° - 170° = 10°

(т.к. сумма углов треугольника равна 180°)

∠DBC = 10°

(потому что он внутренние одно сторонние)

∠B = ∠ABD + ∠DBC = 80° + 10° = 90°

∠C + ∠D = 180°

ΔBCD равнобедр. т.к. BC=CD

(по условию)

По свойству равнобедренного треугольника, углы при основании равны, следовательно

∠CDB = ∠CBD = 10° = ∠C = 180° - 20° = 160°

∠D = 360° - ∠C - ∠B - ∠A = 360° - 160° - 90° - 90° = 180° - 160° = 20°