Вiдстань між центрами кіл, радіуси яких 10 см і 17 см, дорівнює 21 см. Знайдіть довжину спільноï хорди.НУЖЕН РОЗВЯЗОК пж ​

Відповідь:

Довжина спільноï хорди дорівнює 16 см.

Покрокове пояснення:

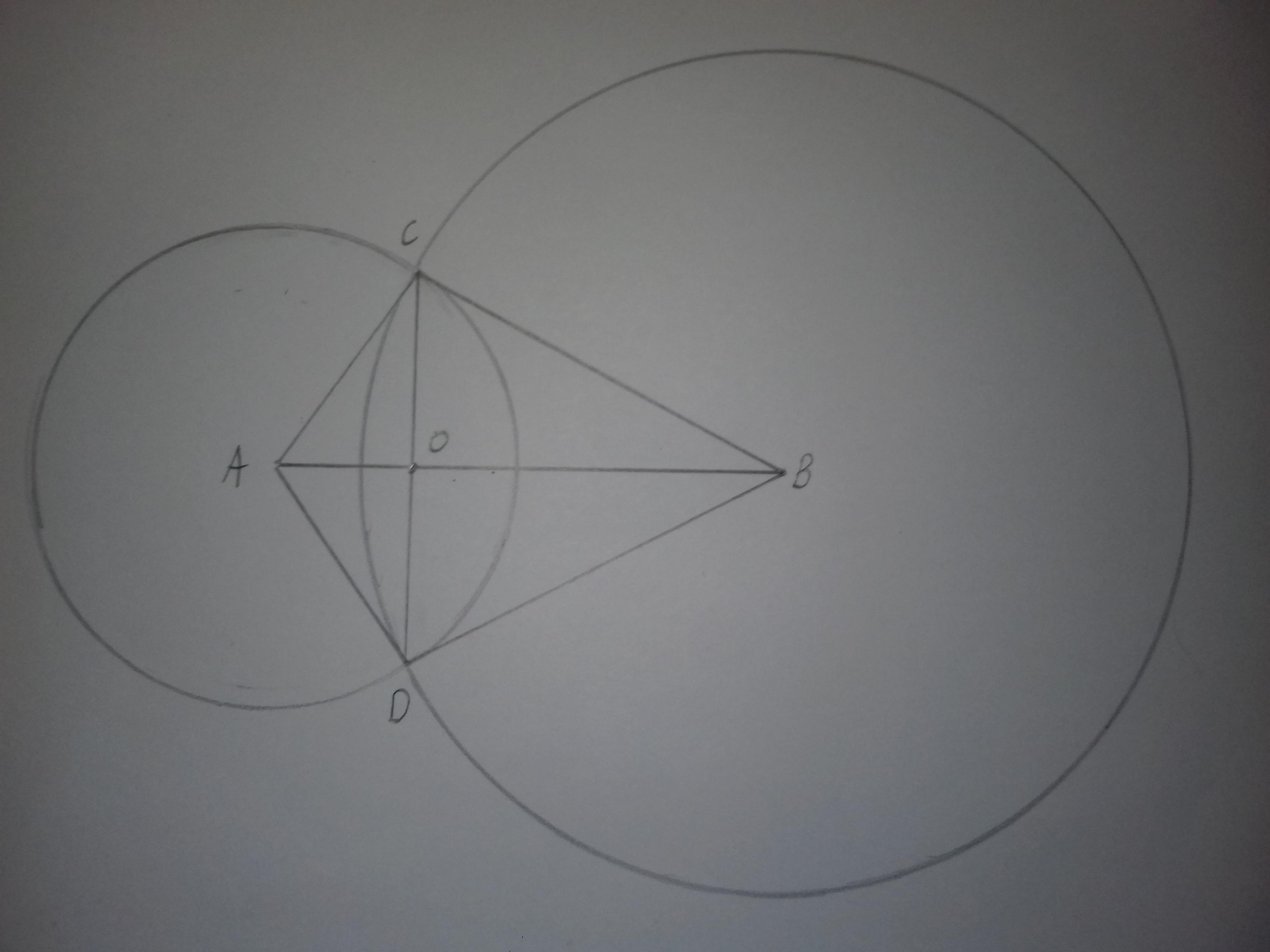
Маємо два рівні трикутники АСВ та АDВ ( АС = АD = 10 см., ВС = ВD = 17 см., АВ = 21 см. - спільна сторона двох трикутників ). СО = DО - це висоти двох трикутників. СD = СО + DО = 2 × СО - хорда, довжину якої потрібно знайти.

За формулою Герона знайдемо площу трикутника АСВ:

Напівпериметр дорівнює:

p = ( a + b + c ) / 2 = 1/2 × (10 + 17 + 21) = 24 см.

Площа трикутника дорівнює:

S = √(p(p - a)(p - b)(p - c)) =

= √(24(24 - 10)(24 - 17)(24 - 21)) =

= √(24·14·7·3) = √7056 = 84 см²

Також площа трикутника дорівнює половині довжини основи помноженій на висоту, що проведена до цієї основи:

S = 1/2 × АВ × СО

Маємо:

1/2 × 21 × СО = 84

СО = 84/21 × 2 = 8 см.

СD = 2 × СО = 2 × 8 = 16 см.