На сторонах AB и BC треугольника ABC взяли точки M и K так, что AM : BM = 1 : 2, BK : CK = 3 : 5. Отрезки AK и CM пересекаются в точке О. Найдите AO : KO.

Ответ:

Отношение AO : KO = 4 : 5.

Объяснение:

На сторонах AB и BC треугольника ABC взяли точки M и K так, что AM : BM = 1 : 2, BK : CK = 3 : 5. Отрезки AK и CM пересекаются в точке О. Найдите AO : KO.

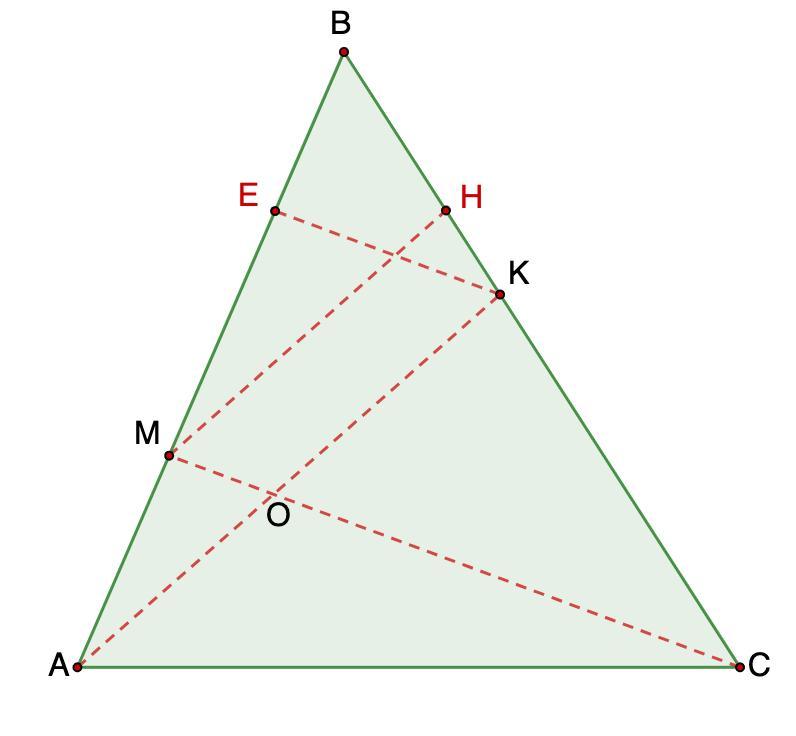
Дано: ΔАВС;

М ∈ АВ; К ∈ ВС;

AM : BM = 1 : 2, BK : CK = 3 : 5;

АК ∩ СМ = О

Найти: AO : KO.

Решение:

Дополнительное построение:

Проведем ЕК || MC; MH || AK.

• Теорема о пропорциональных отрезках:
• Если параллельные прямые пересекают стороны угла, то отрезки, образовавшиеся на одной стороне угла, пропорциональны соответствующим отрезкам, образовавшимся на другой стороне.

1. BK : CK = 3 : 5; ЕК || MC ⇒

Пусть ВЕ = 3х, МЕ = 5х, тогда ВМ = 8х

2. AM : BM = 1 : 2  или

3. MO || EK; АМ = 4х, МЕ = 5х.

Отношение AO : KO = 4 : 5.